-
 @ThothChildren
@ThothChildren
- 2018.5.15
- PV 738
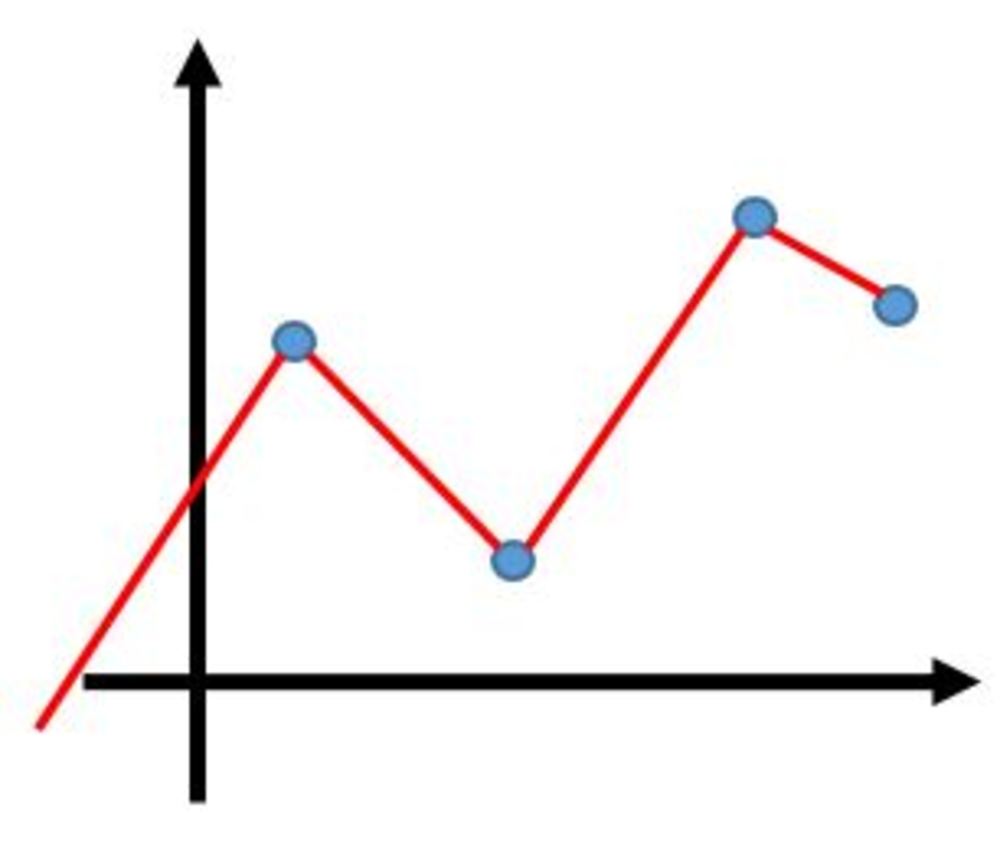
点を参考に滑らかでない関数近似したい
ー 概要 ー
複数のデータ点に沿った関数近似をするときの技術についてです。
精度よく綺麗な関数近似をしたいわけでなく、折れ線近似でいいがすべての点を通るようなものは必要ないときに使える関数近似の手法の紹介になります。
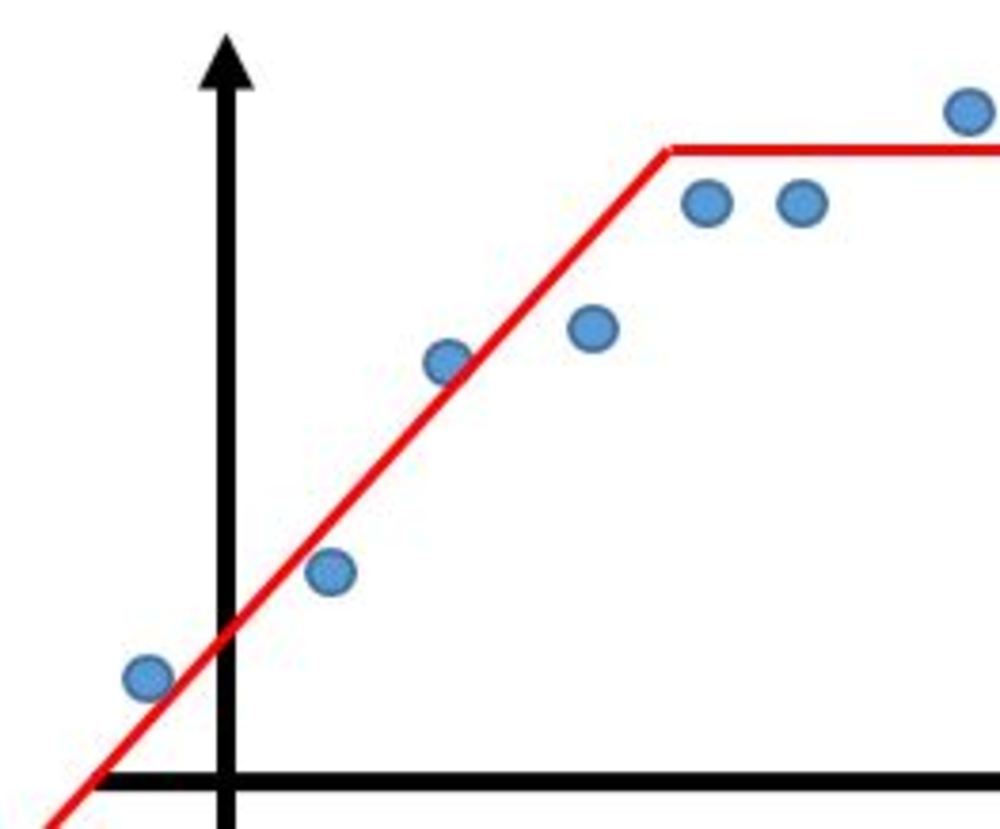
この章を学ぶ前に必要な知識
条件
- 複数の点データ
- 補完したい順番にソートされていること
- 全点を通る必要はない
効果
- 元のデータ点より少ない情報でデータの一連の特徴を表現できる
ポイント
- 各点での傾きは不連続になる
- 折れ点をデータ点から選ぶ場合は、ノイジーなデータでは不安定な近似になりうる
解 説
全点を通る場合は右のリンクを参照.その場合はシンプルな線形近似を行うのみ.
今回紹介するのは、なるたけ使用する点数を抑えて折れ線で近似する手法についての紹介を行う.
今回も折れ線による線形近似にはなるが、全点通る場合と異なり、どのように区間を設定するかが肝となる. | 全点通る滑らかでない関数近似をしたい |
そもそも全点を通らないといっても
・データ点の中から折れ点を選択
・全くデータ点を意識することなく折れ点を選択
の二つが考えられるので注意 | 点の通り方の種類 |
折れ線近似はPolygonal chain applicationなどのようです。 | 折れ線近似の英語 |
1.精度も早さも気にしない場合 | |
精度も早さも気にならずとりあえず折れ線近似して大方を出したい場合は、
以下の方法でよいかと思います. | 精度も速さも気にしない折れ線近似 |
1.始点と終点の点をまず線形近似の一つ目として作成します.
2.その線形近似で誤差が一定の閾値より大きい場合は、始点と終点の間から「中央の点」か「各点を採用したときに折れ線との差が最も小さくなる点」を採用します.
3. 各区分の折れ線近似で2を再度行い、すべての区間で閾値以内になるようにします. | 単純折れ線近似 |
2.において「中央の点」を採用すればかなり単純なアルゴリズムなりますが、それでノイズを拾ってしまった場合には折れ点の数が大きく増えてしまう可能性があります。折れ線近似全般に言えるかもしれませんが、ノイズには弱いです。
各点と線分差の表現はいろいろあると思いますが、L1ノルムでもL2ノルムでもL∞モデルでもよいかと思います。
「各点を採用したときに最も小さくなる点」を見つける場合は全ての点を一度見る必要があるため計算量も増えていきます.
| 単純折れ線近似の特徴 |
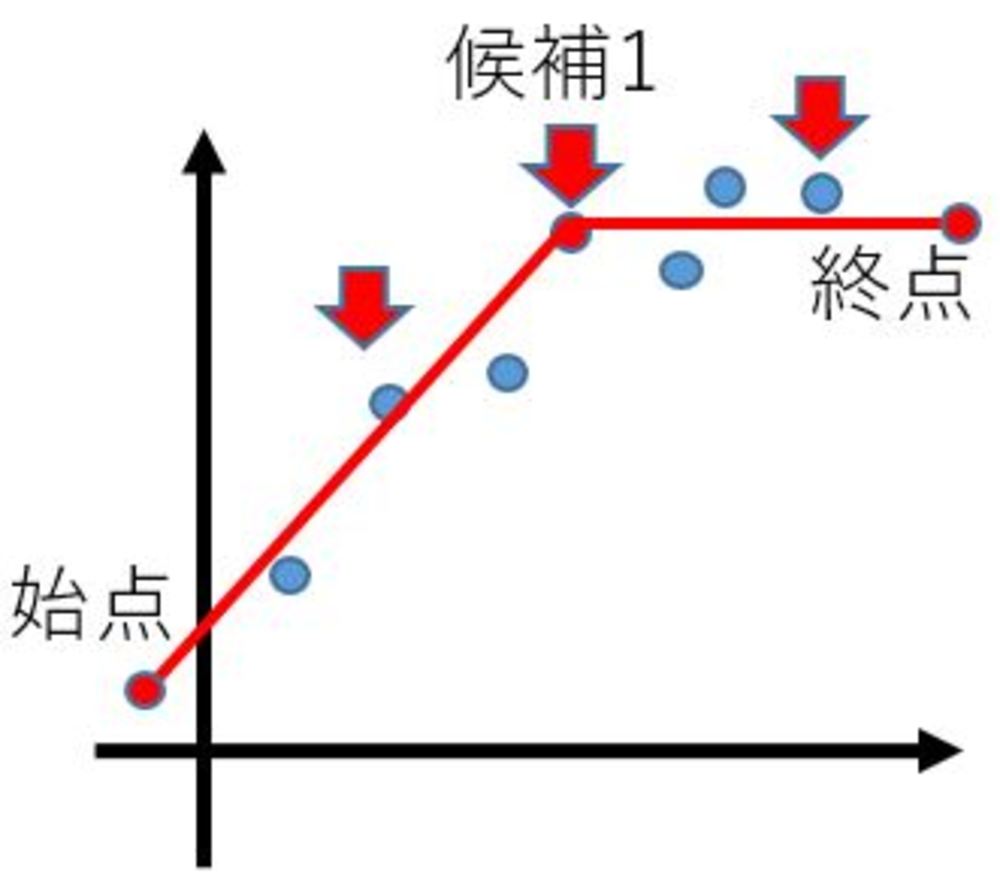 | 単純折れ線アルゴの場合 |
この方法は、Ramer–Douglas–Peucker アルゴリズムと呼ばれる.(単にDouglas–Peucker, RDPとも呼ぶ)
この関数の差分はハウスドルフ距離を用いて近似曲線と元の曲線の差の評価を行っている. | 外部リンク Ramer–Douglas–Peucker アルゴリズム(英語) Wikipedia |
右のリンクの論文では、閾値を自動決定することによって入力データによって適応的に折れ線の具合を調整するアルゴを発表している.
気になる場合は参考にしてほしい. | 外部リンク A Non-parametric RDP Algorithm Based on LeapMotion(論文) |
2.単純だがO(n)で近似できる折れ線近似 | |
 | Reumann-Witkamアルゴリズムによる折れ線近似 |
ここで紹介するアルゴリズムも単純なアルゴリズムで、恐らく容易に想像がつくものになるかと思います。
Reumann-Witkamと呼ばれるアルゴリズムであり、単純でありながらO(n)で計算が完了します。
アルゴリズムは、
1. 折れ線からはみ出てもよい閾値を決めて、末端の一つを始点、もう片方を終点とします.
2. 始点から次の点の方向に直線を伸ばしていき、閾値を外れる点が出てくるまで伸ばします.
3. 折れ線と元の点の差が閾値を超えた場合にその区分の直線は終了して、最後に折れ線を張ったところから次の点に直線を延ばしていきます.
4. 終点になるまで2.と3.を繰り返します.
| Reumann-Witkamのアルゴリズム |
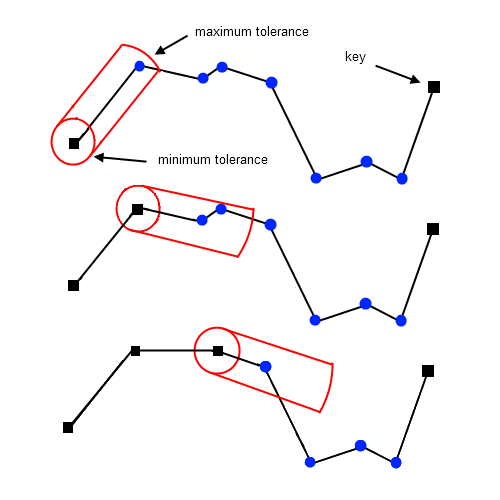 | Opheimというアルゴリズム同様な方法で線を見つけることができます. |
上記で紹介した折れ線近似では、直後の点を参考に補間を伸ばしていくため、
精度が悪化しやすくなります。データ点の変動が激しい場合はほとんどの点を削ることなく近似が完了することになりえます. | 上記で紹介した近似 |
3.やや遅いが精度が少しよい方法 | |
Langのアルゴリズムを用いた場合は、O(n)にはなりませんが、線の特徴を効率よく残しながら折れ線近似をすることが可能になります。
Langであらかじめ決めるべきは「いくつ先まで見るか」と「折れ線からどの程度はなれる点まで許容するか」です. | やや遅いが精度が少しよい方法 |
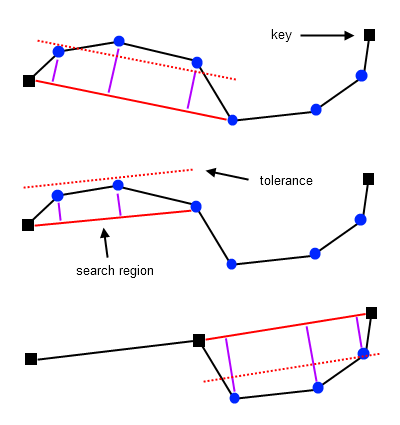 | Langアルゴリズム |
1. 先に「いくつさきを見るか」を決めておき、始点と終点も決めておく.
2. 開始点とそこから「いくつさきを見るか」分先の点で仮に直線を決めます.
3. そのときにその間にある点が適切にsearch region以内に収まっているか即ち閾値以内か確認します.
4. もし閾値以内でない場合は、一つ手前の点と開始点で直線を引きなおして再度確認します.
5. 4.を繰り返して間の点が全て閾値以内になるか、開始点の次点になるまで行います.
6. 5.で点の選択が完了したら、その点を新しい開始点として再度2.から行います. | Langアルゴリズムの概要 |
4.精度よく比較的高速な方法 | |
右の論文に記載されているL∞折れ線近似アルゴリズムについて紹介する.
点列を誤差許容範囲分上下y方向に水平移動させた点列によって囲まれた領域を考える.
不可視な領域の一点となっている点を通るような線分を引いていくことによって最小の数で線分を引くことが可能となる. | 外部リンク 折れ線近似に関する修論 |
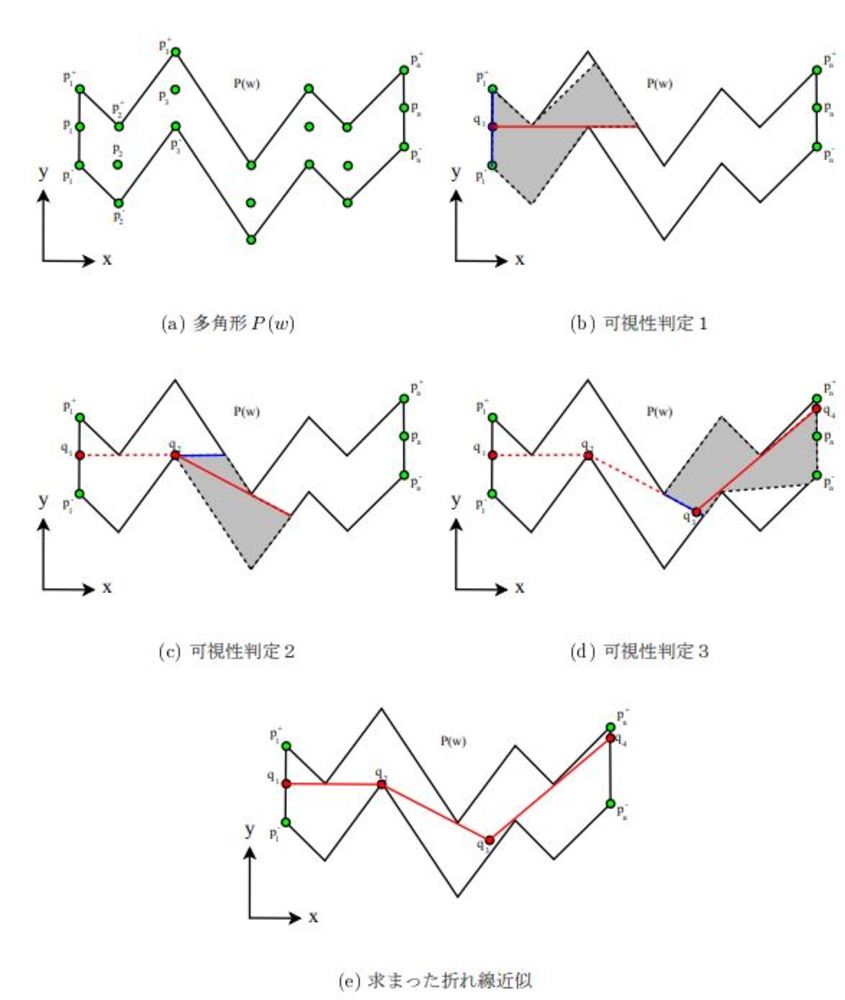 | 論文より引用したL∞折れ線近似アルゴリズムの図解 |
ハウスドルフまたはフレシェ誤差を用いて線形な近似アルゴリズムを提案してものもあり、速度や精度の面で秀でています.
| 外部リンク Near-Linear Time Approximation Algorithms for Curve Simplification |
この章を学んで新たに学べる
Comments