-
 @ThothChildren
@ThothChildren
- 2018.5.16
- PV 1170
関数既知で多数データの関数近似したい
ー 概要 ー
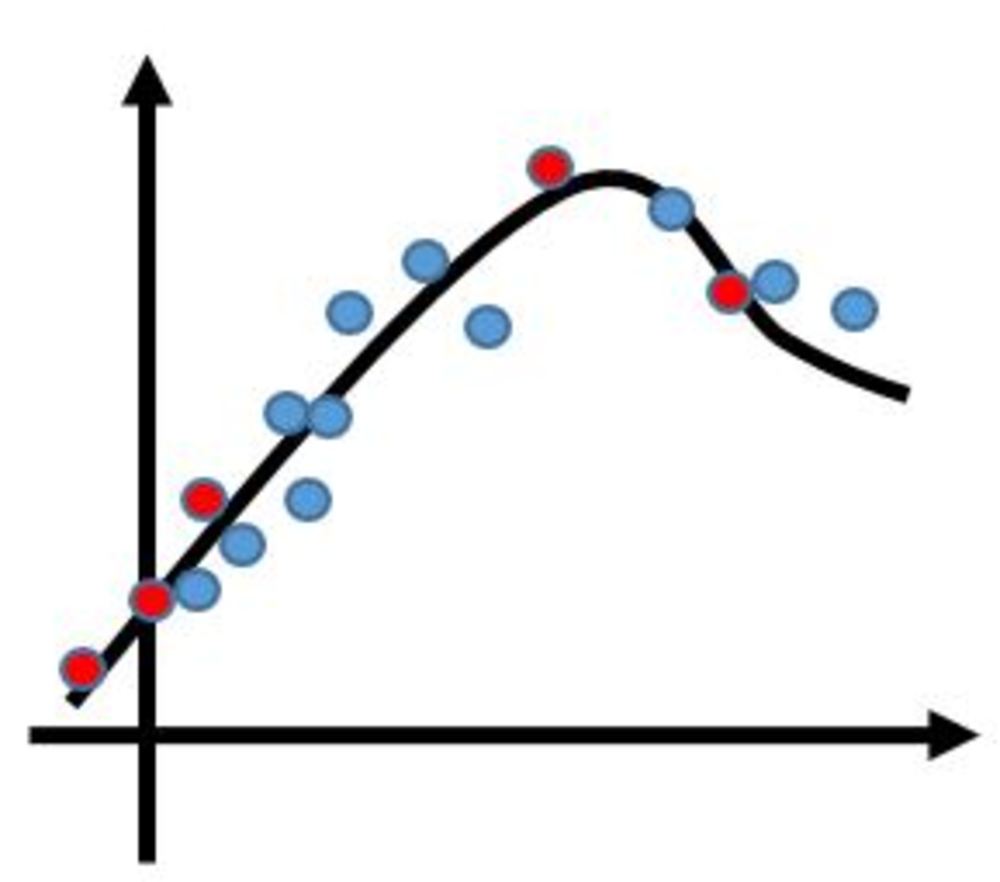
データの当てはまりがよさそうな関数が既知で多数のデータが与えられるときに、それらのデータを用いて関数近似をする方法についてまとめます.比較的単純で代表的な技術のみにとどめます.
この章を学ぶ前に必要な知識
条件
- データの当てはまりが良さそうな関数が分かっている
- あとは関数の係数を求めるのみ
- 十分なデータ数
効果
- データをよく表現する近似関数を得る
ポイント
- 最小二乗法とRANSACとハフ変換について紹介
解 説
データの点の集まりからどのような形の関数であるかは分かっているが、
どういった係数になるかを求めたいときに使用できる技術について紹介する.
どれも関数の形状が決まっていることが前提となっている.
・最小二乗法
外乱に弱く、外れ値があると想定しない近似になることがある
・RANSAC(Random Sample Consensus)
外乱には強いが、パラメータの数によっては処理が遅くなりがち
・Hough変換
外乱に強いが、複数候補がある場合閾値での対応がしにくい
| 関数既知で多数データの関数近似したい概要 |
1.最小二乗法 | |
最小二乗法は関数のフィッティングにおいて頻繁に使用される代表的な方法.
解析的に解け、最小値が計算をすぐに求めることができる
発想は比較的シンプルで、「データ点と関数の誤差の二乗和」を最小にする関数の係数を求める. | 外部リンク 最小二乗法 |
 | Jが誤差の二乗和(Wikipediaより引用).
この値を最も小さくすることで関数がデータによく当てはまっていると言うことができそう |
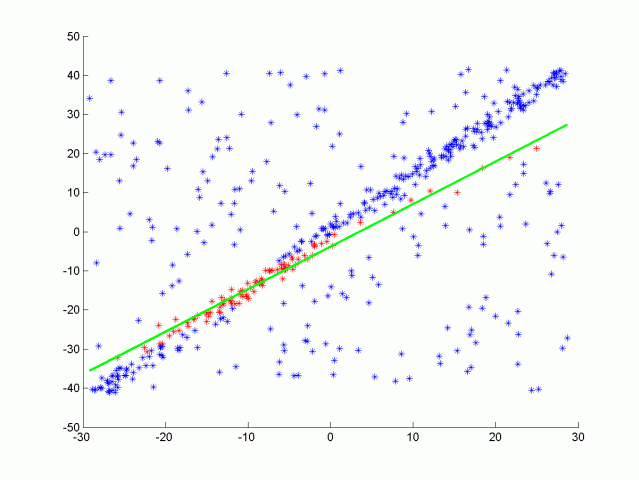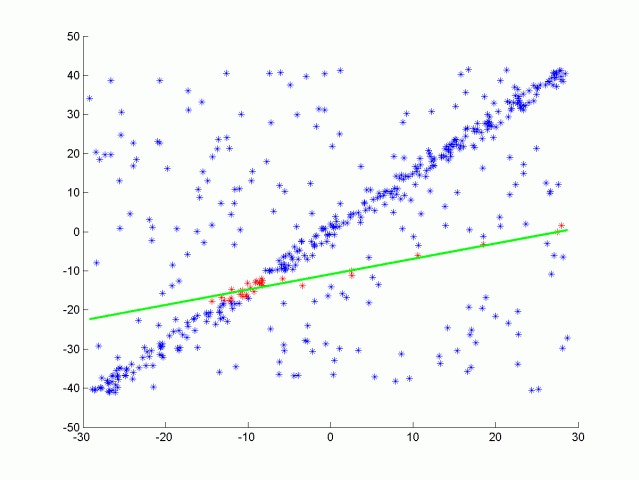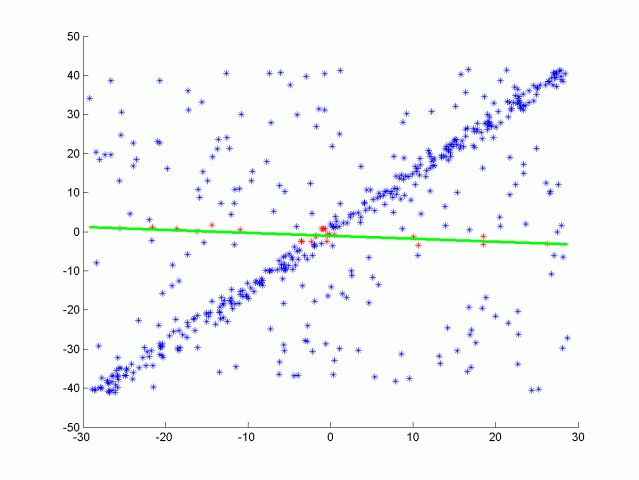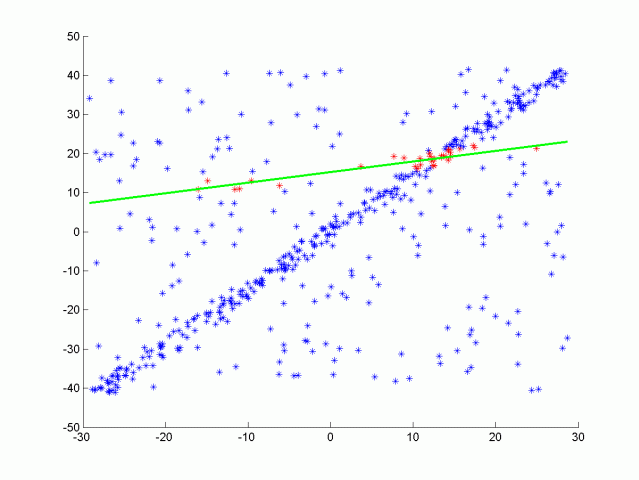
しかし、最小二乗法は全体の誤差を小さくするように動くため、大きく外れた外れ値がある場合はそれに引っ張られて思った関数と違った関数になってしまうことがあります. | 最小二乗法の欠点 |
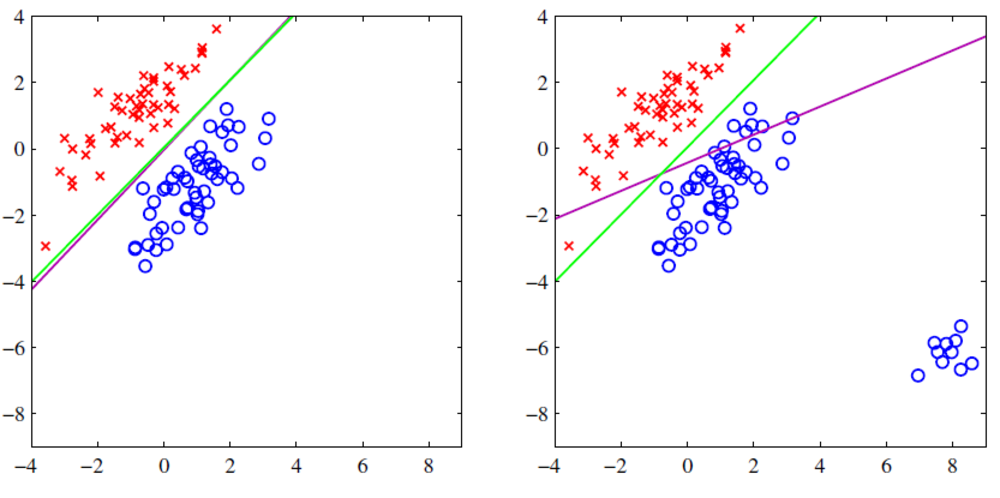 | 右側の画像が外れ値がある場合.紫の直線が推定結果で、大きく関数が逸れてしまっている。 |
最小二乗法の改良は多くがあるがいくらかのみ簡単に列挙しておく.
・Total Least Squares
Total Least Squaresは通常の最小二乗法がy-f(x)を行っている差分の出し方ではなく、ちゃんとfの関数に(x,y)からの距離の差分を出すことで精度向上を狙う.
・ロバスト推定
外れ値の影響を受けやすい最小二乗法を改良して、反復的に計算することで外れ値に影響されにくい係数を求める.
初めに最小二乗法を計算した後に、そこでの誤差が大きいものの重みを下げて以後反復的に最小二乗法を繰り返していく.
| 最小二乗法の改良 |
2.RANSAC | |
RANSACは、何度もランダムに点をサンプルして最もよい関数を探索するアルゴリズム.
<手順>
1. データ点をいくらかサンプルし、それに対してフィッティングを行う.
2. フィッティングの関数でデータとの誤差を算出
3. 2.を繰り返した後に最も誤差が少ない関数を採用 | 外部リンク RANSAC(英) |
 | RANSACを実行しているGifアニメーション.外れ値に非常に強い. |
RANSACは上記のようにノイズに強い手法である.
しかし、一方で何度も計算を行うため遅くなりがちというのが気になる点.時間を掛けるほどよい関数が得られる可能性が高く、逆に短いと精度が悪化する可能性がある.
RANSACにおいては複数の候補があるときに閾値を決定しにくいという欠点も持つ. | RANSACの特徴 |
3.Hough変換 | |
Hough変換は何度もあるデータ点を取り出してそれに対する関数を求めたときに、
その係数を集計して最もよさそうな係数に投票するアルゴリズム.直線以外の円などにも適用でき、一般ハフ変換が発明されている.
<手順>
1. 二点取り出して直線を求めて、係数を算出.
2. 1.を繰り返して係数の候補をためていく.
3. 2.でためた候補をプロットして投票を行い、最も候補としてふさわしい係数の組み合わせを採用する.
| ハフ変換概要 |
 | ハフ変換による処理の過程
右側に投票を行っており,最終的に選択する係数の組み合わせを決める |
ハフ変換を用いることで、ノイズに強い関数を推定しやすくなる.直線の特徴の一部がたとえ隠れていたとしても適切に検出できるのが強み.
実装の工夫として係数がピッたしに一致することはないので、ある程度許容した状態で投票をしてもらう必要あり.
| ハフ変換特徴 |
この章を学んで新たに学べる
Comments


