-
 @ThothChildren
@ThothChildren
- 2018.5.16
- PV 228
関数未知で多数データの関数近似したい
ー 概要 ー
関数未知な状態で多数のデータがある場合の関数近似を行うときの手法について書いてみます.関数が未知なので表現力のある手法が必要になります.
この章を学ぶ前に必要な知識
条件
- 関数は未知の状態(既知でも適用はできる)
- 関数を推定するのに十分なデータ量
効果
- データから関数を推定する
解 説
関数が未知な状態で多数のデータを得られるときの関数近似を行う方法について紹介します.
ここでは以下二つを紹介する.他にも紹介できるものがあれば随時追加していく.
・ニューラルネットワークによる関数近似
・Gaussian Process(ガウス過程)による関数近似 | 関数未知で多数データの関数近似したい概要 |
1.ニューラルネットワークによる関数近似 | |
ニューラルネットワークは、単層では線形的な表現しかできないが、多層ニューラルネットワークにすることで理論上(長大なネットワークにすれば)、任意の非線形な関数を表現できることが知られている.
このとき、非線形な活性化関数をいれなくては多層にしても線形の表現しかできないので要注意.
ニューラルネットワークによって関数近似をするには、多量のデータ点をニューラルネットワークに学習させ、入力に対して適切な写像ができるようにすることで可能となる. | ニューラルネットワークによる関数近似概要 |
欠点
・学習データ量とパラメータによっては過学習になってしまう.
また、精度の保障等もできない.
| ニューラルネットワークの特徴 |
ニューラルネットワークによる関数近似の実験.
少しずつ関数近似ができている様子が分かる | |
2.GaussianProcessによる関数近似 | |
GaussianProcessはカーネル法をベースに関数近似を行う手法.カーネル法になるため、データ点が関数に含まれる形になり、パラメータ数はデータのサンプル数に比例するのが特徴.
学習データが少ないときにもノイズに対して過学習することなく、関数近似を行うことができる.
| GaussianProcessによる関数近似概要 |
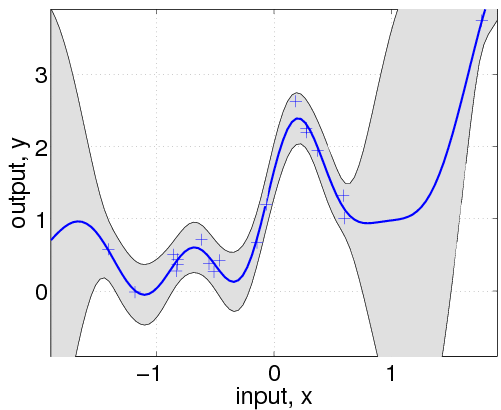 | GaussianProcessの図.灰色は分散部分を示している.+がデータ点になっているが、データ点がある部分では分散が小さくなっている. |
この章を学んで新たに学べる
Comments


