-
 @ThothChildren
@ThothChildren
- 2018.5.17
- PV 176
無限の多項式で関数近似する
ー 概要 ー
無限の多項式の和によって特定の関数の近似を行います.ここでは特にテイラー展開について紹介します.
この章を学ぶ前に必要な知識
条件
- 関数によってはある点の周りでの展開となる
- 関数が無限回微分可能であること
効果
- べき級数の形で表現される関数が得られる
ポイント
- 主にテイラー展開の紹介
解 説
無限の多項式の和で目的の関数f(x)を近似する方法について紹介する.
\(f(x) = \frac{1 }{1-x}\)
のような関数は\(f(x) = 1 + x + x^2 + \ldots\)であることが知られている.
これは通常の関数をべき乗級数の形で記述したものであるが、
このような形でない関数も条件も満たせば多項式の形に展開することができる. | 無限の多項式で関数近似する |
1.テイラー展開 | |
 | テイラー展開の式
x=aでの展開時は左記のような関数になる |
テイラー展開について詳しくは右のwikipediaを参照願います.
ここでは簡単に説明するのみとどめます. | 外部リンク テイラー展開 |
テイラー展開を用いると\(x = x_0\)の点の近辺でよく近似した関数を得ることができる.
上記の\(x=x_0\)の周り以外でテイラー展開をした関数を使うと大きく値が外れてしまうことがあり,どうすれば問題なく使用できるかは収束半径による.
関数によっては\(x = x_0\)の周りでなくても適切に展開することができ、特に
・\(e^x\)
・\(sin(x), cos(x)\)
はどのような入力に対しても使用できる.
| テイラー展開の紹介 |
上記がx=aにおけるテイラー展開の関数になっている.
多項式をテイラー展開しようとする場合、自分自身のテイラー展開の値を得る.微分すると0になることである項以降は項が存在しえない.
上の式においてa=0としてものをマクローリン展開と呼ぶ.
| テイラー展開の特徴 |
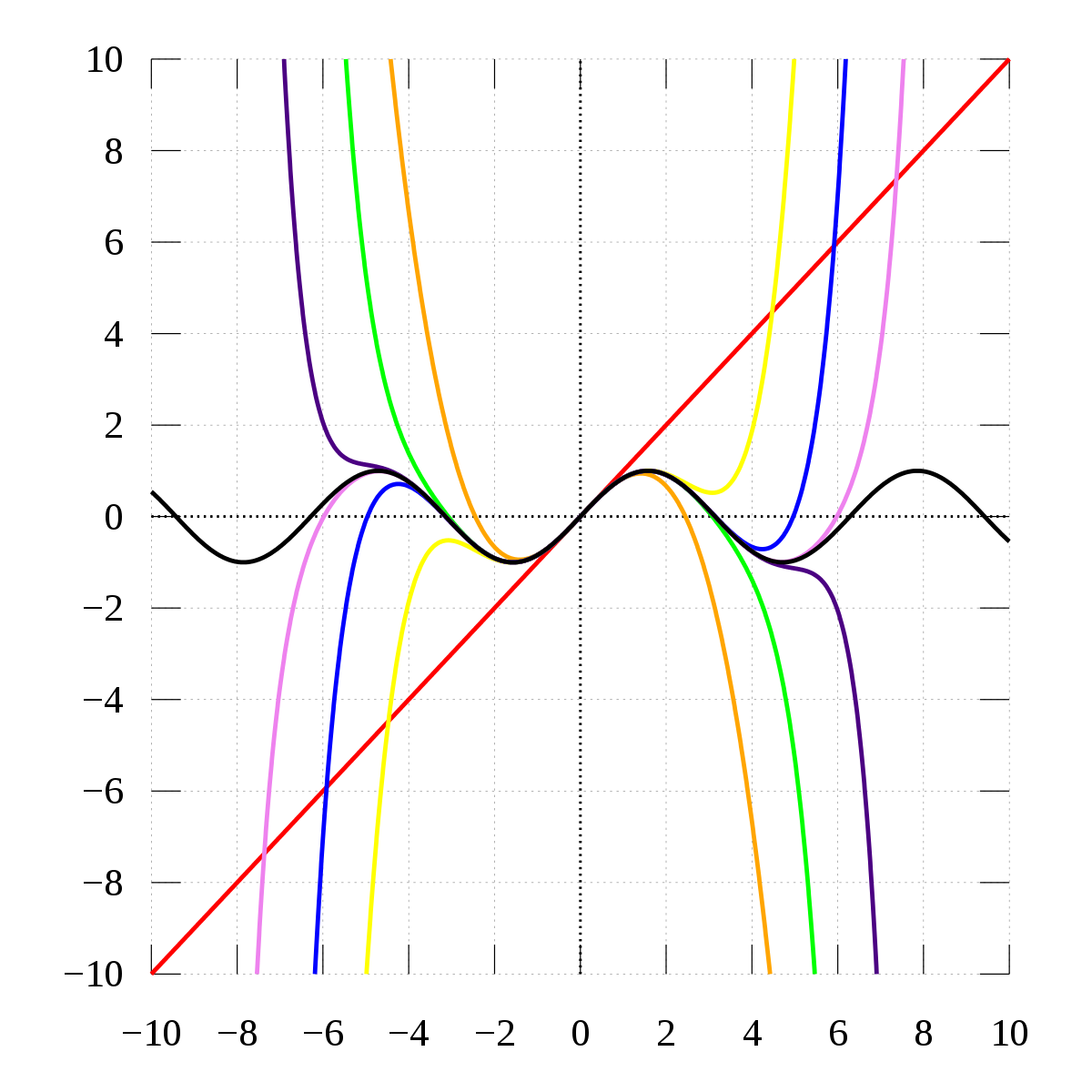
Cosを実際にテイラー展開しているときの図.
1項ずつ足したときにどのようになっていくかを確認できる. |
この章を学んで新たに学べる
Comments


