分布に従った乱数生成関数を書きたい

ある分布に従った乱数生成関数をプログラムで書く方法についてまとめます. 多くの有名な分布に関してはそれぞれやり方が求められていますが、自身が用意した確率分布に対してその分布を生成するプログラムを書きたいときに参照してください. 主な方法は二つあります. ・本当に一様確率のもとでその事象を起こしてみる. ・分布関数の逆関数を求める になります.

これは愚直な方法で処理時間も一定にはなりませんが、直感的にプログラムをかけるケースがあります. それは確率分布の定義に基づいて実際に試行してみる方法です. 例えばわかりやすいケースは幾何分布になります. 幾何分布に従う乱数を生成したい場合は、幾何分布がそもそも確率pで起こる事象がn回目に初めて起こるときの確率であったことを思い出してそれを実際にやってみればいいのです.

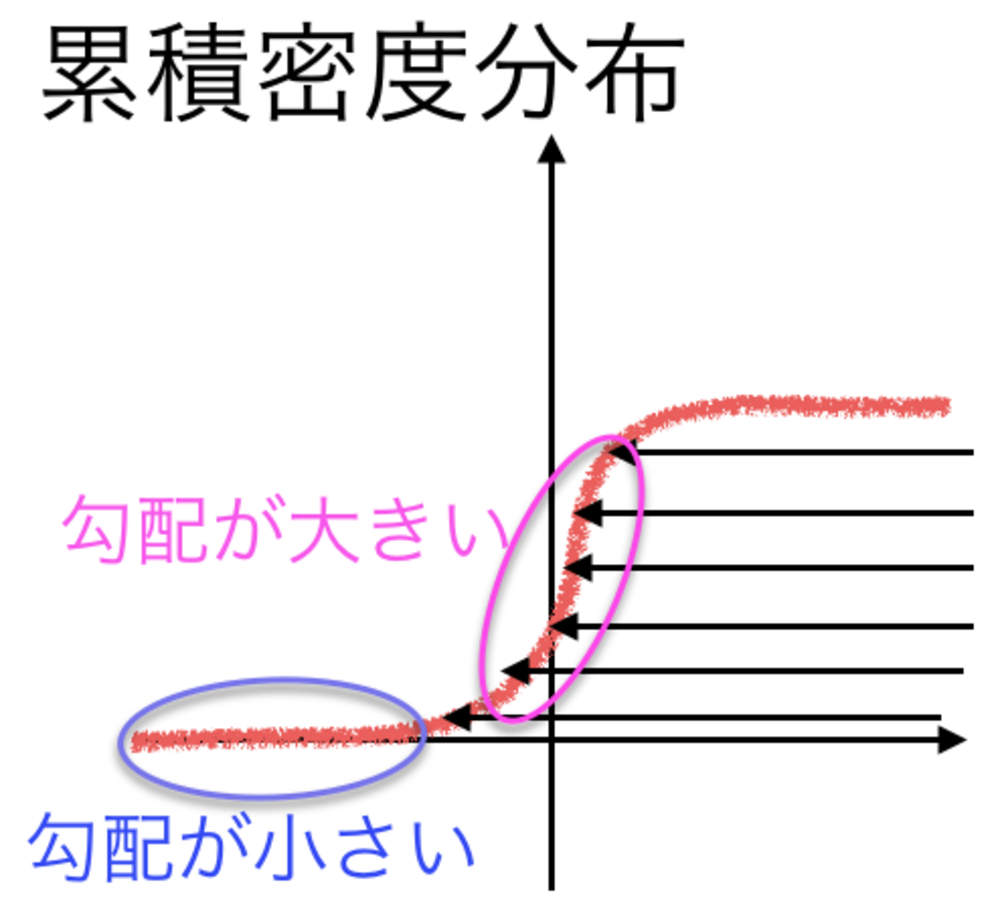
もう一つの正当な方法の一つは逆関数を求めて乱数を生成する方法です. 累積分布関数は密度分布を積分することによって求めます. 累積分布関数を作るとその値は単調増加していることがわかり、また密度関数の値が大きいところで大きい傾斜になっていることがわかると思います. このときyの値を決めればそのxの値が得られることになりますが、急な勾配であるところのほうがその近辺の乱数が多く得られることを示します.すなわち適切にそのxの値になる確率が高くなるようになっているのです. ワイブル分布やロジスティック分布などに関してはこの方法によって求めることができます.