三次方程式を公式で解きたい

三次方程式の解はカルダノの公式によって求められることが知られている.

カルダノの公式に関する詳しい導出は左のリンク先を参照してください.

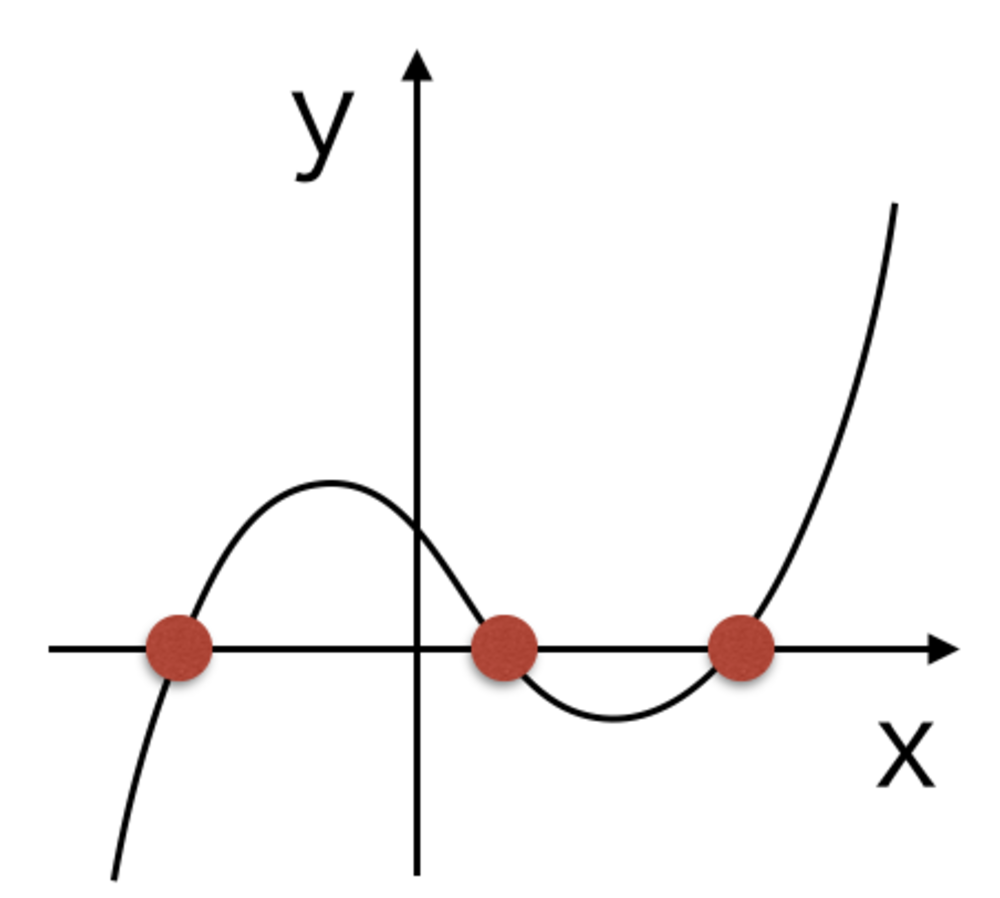
公式によって複素数も含めて3つの解を得ることができる. 3次関数が必ず1点以上でy = 0と交わることを考えれば当然だが、 この公式では必ず一つ実数の解を得ることができる. 逆にy=0で1つしか交わっていないとき、残り二つの解は複素数となり、 y=0で2点なら重解を含む2つの解と3点なら３点の実数の解を得られることになる.

$$ (\frac{q}{2})^2 + (\frac{p}{3})^3 < 0$$

上記の式は3つの実数解を持つための判別式. 二次関数のときの判別式は平方根の中が正になるb^2-4ac > 0であったが、 3次関数のときの判別式は平方根の中が負になることで3つの実数解が持つことが保障される.

$$ y = \omega^k\sqrt[ 3 ]{ -\frac{q}{2} + \sqrt{((\frac{q}{2})^2 + (\frac{p}{3})^3)} } + \omega^{3-k}\sqrt[ 3 ]{ -\frac{q}{2} - \sqrt{((\frac{q}{2})^2 + (\frac{p}{3})^3) }}$$