-
 @ThothChildren
@ThothChildren
- 2018.6.17
- PV 1276
二次元点群から凸包を求めたい
ー 概要 ー
二次元座標上に散らばる点群から凸包を求める方法についてまとめたページです.凸包は与えられた点の中から如何に凸包の候補でないものを削っていくかが高速化のポイントになります.手法の違いは計算量と実装の容易さに現れています.
この章を学ぶ前に必要な知識
条件
- 入力は二次元座標を持つ点列
効果
- 二次元座標の点列を内包する凸包
ポイント
- 複数のアルゴリズムの違いは計算量
解 説
二次元座標を持つ点列から凸包を求めるアルゴリズムについてまとめています.
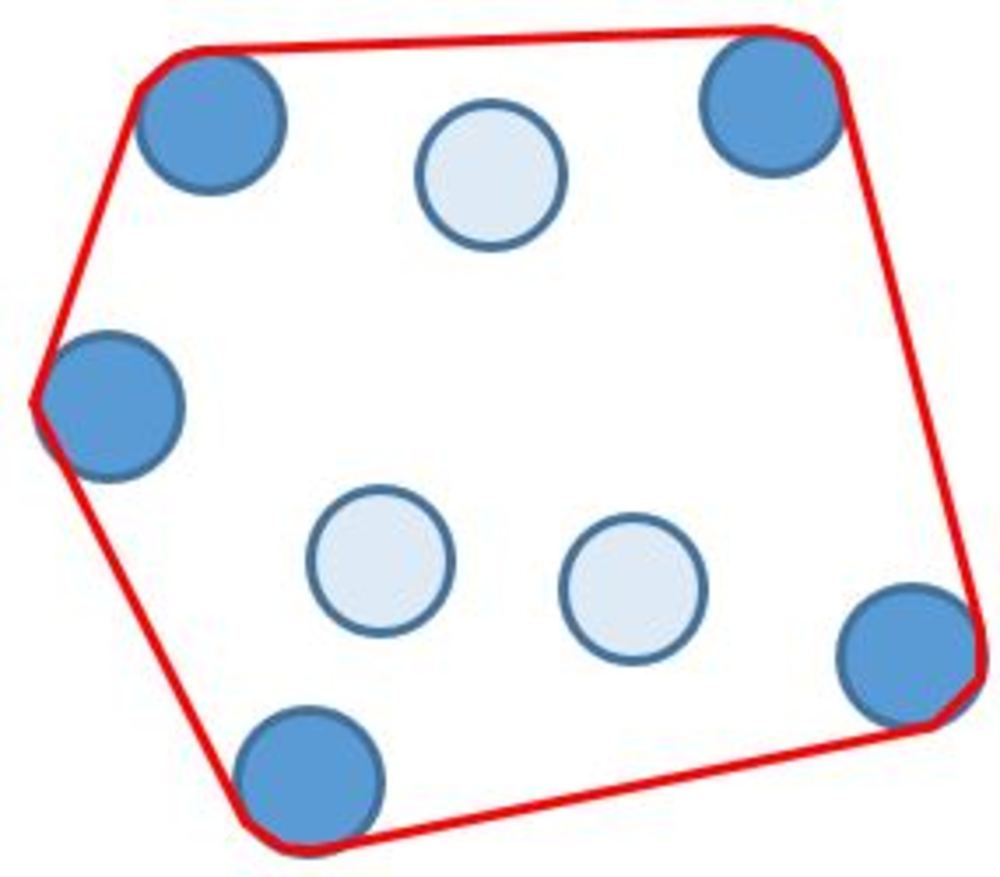
そもそも凸包とは上記の絵にあるように複数の点を全て内包する最小の図形になります.
ただその表現だけでは実は正しくなく、その図形は
凸包では凸包内のいかなる二点同士を結んでその線上に点を決めてもそれは凸包の中にあるという性質も持っていなくてはいけない.つまり凸包の全ての頂点は外側に出っ張ってるってだけですが...
凸包を見つけ出すアルゴリズムは与えられた点の中から凸包の点になる候補を見つけていくのが流れです.またそれを如何に早く候補を絞っていくかが大切です.
点の候補を絞るときに役立つこと
・選んだ3点の三角形の中に含まれる点は凸包の頂点ではない.
・ある座標軸(x軸やy軸)で最大最小となっている点は凸包の頂点.
・初めにx軸の最大最小とy軸の最大最小で結ばれる四角形の中の点を候補から外すと一般的に早くなる
| 二次元点群から凸包を求めたい |
凸包を求めるアルゴリズムは以下のように幾らかあります.
以下ではnは点数、hは凸包に含まれる点数.
・特定の三点を選んでその中に含まれている点を除去を繰り返す
O(n^4)となるシンプルで最も遅い方法.三角形の中に含まれる点は凸包の頂点の候補にはならないため、除去できます.
・ギフト包装法
シンプルで有名な方法.O(nh)で見つけられるが、最悪ケースではO(n^2).凸包の頂点を一つ見つけたら、次に結ぶ点の片方の側に点が存在しないように点の選択を繰り返す方法.
・Grahamの方法
点を円周方向にソートした後に、順に凸包に含まれるかどうかを判定していきます.ソートでO(n*log(n))で判定でO(n)のため、全体としてはO(nlog(n))になります.
・QuickHull
高次元でも使用することのできる凸包アルゴリズム.Quickソートのような動きをして、凸包を求めていく.O(n log(n))だが、最悪ケースではO(n^2)となる.
・分割統治法
小さい点群で凸包を求めてそれを統合していく方法.
・逐次構成法
一点ずつ点を加えていく方法
・Kirkpatrick-Seidelの方法
O(n log(h))な高速な手法. しかしやや複雑な動きをする.
・Chanのアルゴリズム
上記のKirkpatrick-Seidelと同様な方法だがかなりシンプルになっておりこちらもO(n log(h)) | 凸包を求めるアルゴリズム |
凸包のアルゴリズムについては解説しているページが多いため、
以下では有名なもののみ紹介します. | 紹介するアルゴリズム |
1.ギフト包装法 | |
 | ギフト包装法のGifアニメーション
(https://en.wikipedia.org/wiki/Gift_wrapping_algorithm より引用) |
アルゴリズムはシンプルで
1. 最もx座標が小さく、その中でyも最も小さいものを求めて注目点とする
2. 次の点を求めるために、注目点ほか全ての点との偏角を求めて、最も左にあるものを選ぶ.
3. 一周するまで繰り返す.
辺の数が点数より圧倒的に少ない場合は、他のアルゴリズムでも同等の性能を出すことができる.しかし、そういった縛りがないときや最悪ケースでは計算量が増えてしまう. | ギフト包装法 |
2.Graham Scan | |
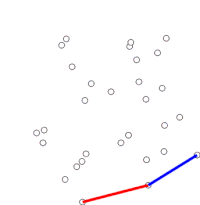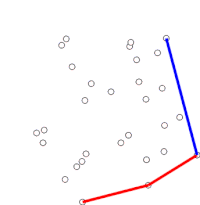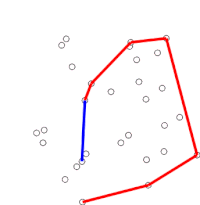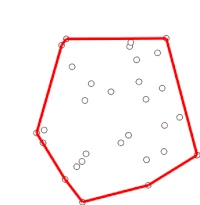 | Graham ScanのGifアニメーション
(https://en.wikipedia.org/wiki/Graham_scan より引用) |
Grahan Scanのアルゴリズムもシンプルです.
1. まず凸包の候補となる点をx,y軸の最大最小から選びます.(最初の注目点)
2. その点を基準にある中心に沿って角度で点をソートします(n log(n). 計算量の支配項)
3. 現在の注目点からソートされた点を追っていきます.次の点にとりあえず線を延ばします.(上図のような反時計回りで追っていきます)
4. さらに次の点に伸ばしたときに先に延ばした線よりも右側に来たとき、一つ前が凸法の候補でなかったことがわかります.
5. 一つ前と二つ前で引いた線を消し、今回と二つ前の間に直線があるとします.
6. 初めの点に戻るまで3~5を繰り返します. | Graham Scanのアルゴリズム |
Graham Scanでは角度でソートを行いましたが、xでソートをする手法もあります.
Monotone Chain Algorithmではxでソートして対象の上側と下側に分けてそれぞれで凸包を求めます. | Graham Scanと同様な考え方 |
3.QuickHull | |
 | QuickHullのアルゴリズム
(https://en.wikipedia.org/wiki/Quickhull より引用) |
QuickHullは少々特殊なソートを行う手法です.
基本はある線を引いたときに最も離れた点を凸包の新しい点として加えていくことを繰り返します.
通常の計算量はO(n log(n))ですが最悪計算量においてはO(n^2)となります.
1. x座標の最大と最小の点を見つけます.(注目点とする)
2. 注目点間で線を引き、その点から最も離れた点を候補とします.
3. 最も離れた点と線の中の三角形に含まれる点を候補から除外します.
4. 上記の三角形の辺から最も離れている点も凸包として追加し2から再度繰り返します.
5. 点が残ってなければ完了 | QuickHullの詳細なアルゴリズム |
この章を学んで新たに学べる
Comments


