-
 @ThothChildren
@ThothChildren
- 2018.6.19
- PV 659
一筆書きができるパスを見つけたい
ー 概要 ー
一筆書きができるパスを見つけるアルゴリズムについて紹介します.有名なのはFleuryのアルゴリズムです.
この章を学ぶ前に必要な知識
条件
- 頂点とエッジからなるグラフ
- 奇数本のエッジをもつ頂点は2つまたは0
効果
- 一筆書きができるパスを与える
解 説
一筆書きができるパスを見つける方法についてまとめます.
一筆書きができるグラフのことをオイラー路と呼びます.また始まった頂点と終わる頂点が一致するものをオイラー閉路といいます. | 一筆書きができるパスを見つけたい |
一筆書きができるパスを見つけるためには、そもそも一筆書きができる経路でないといけません.それは経路を見つける前に判定することができます.判定方法は右のリンクを確認ください. | 一筆書きで書けるか判定したい |
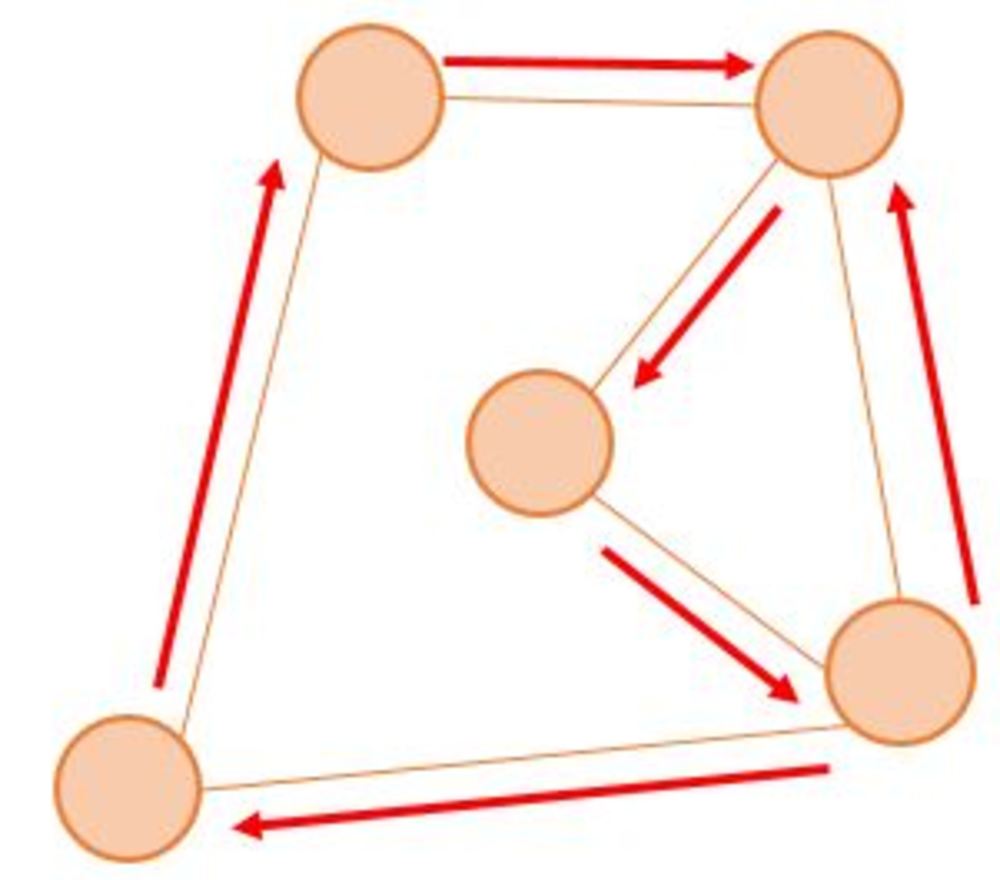
一筆書きのパスを見つけるFleuryのアルゴリズムについて紹介します.
ルールはかなりシンプルです.
アルゴリズム
1. 適当な頂点から開始して、通った辺を消していく
2. 通る辺を選ぶときは、その辺を消してもグラフが二分されない辺を優先的に選んでいく. | Fleuryのアルゴリズム |
実装を含めてより詳しい情報は貼り付けたリンク先で説明されていますので、参考にしてみてください.(英語です) | 外部リンク Fleuryアルゴリズムの解説 |
このアルゴリズムは、辺の数をEとするとO(E^2)となります. | Fleuryアルゴリズムに関して |
1.Hierholzerのアルゴリズム | |
Hierholzerのアルゴリズムは、先のFleuryのアルゴリズムがO(E^2)であったのに対して、頂点の数をVとしてO(E+V)となっており、若干高速になっています.
手順
・ある点から初めてまたその点に戻るパスを見つけて通ったパスを除去していきます.
・上記を繰り返してできた複数の閉路をつなぎ合わせます.
つなぎ合わせによって一筆書きができるようになります. | Hierholzerのアルゴリズムについて |
Hierholzerについてもう少し丁寧な解説は右参照 | 外部リンク Hierholzerアルゴリズムの解説 |
この章を学んで新たに学べる
Comments
Reasons
知識: 一筆書きで書けるか判定したい
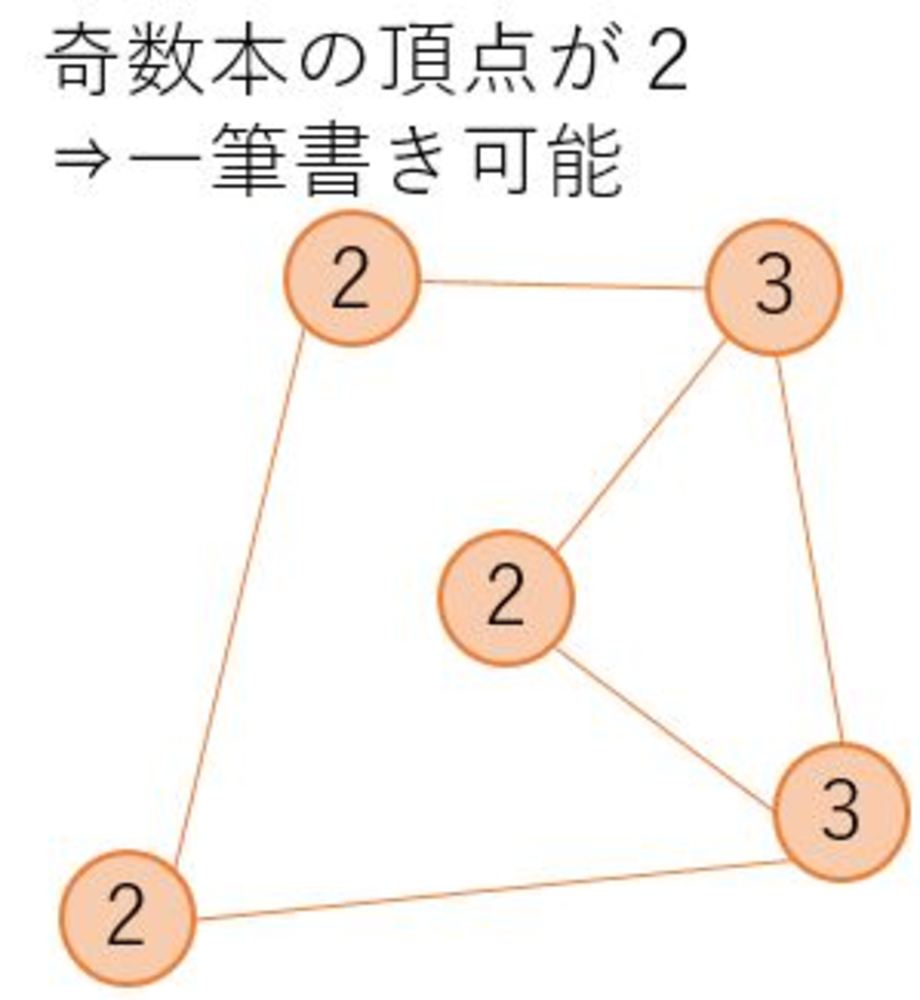
一筆書きである線の経路をなぞれるかどうかを判定したいときに使える方法について紹介します.一筆書きできる経路のことをオイラー路といい、辺をたどったら始点に戻るものを特にオイラー閉路と言う.


