-
 @ThothChildren
@ThothChildren
- 2018.7.7
- PV 1275
ヘッセ行列
ー 概要 ー
多変数関数f(x_1, x_2, x_3....)のような関数を各x_1, x_2...で二階微分を行い行列としたものをヘッセ行列という.極値の判定やニュートン法における近似解導出に用いられる
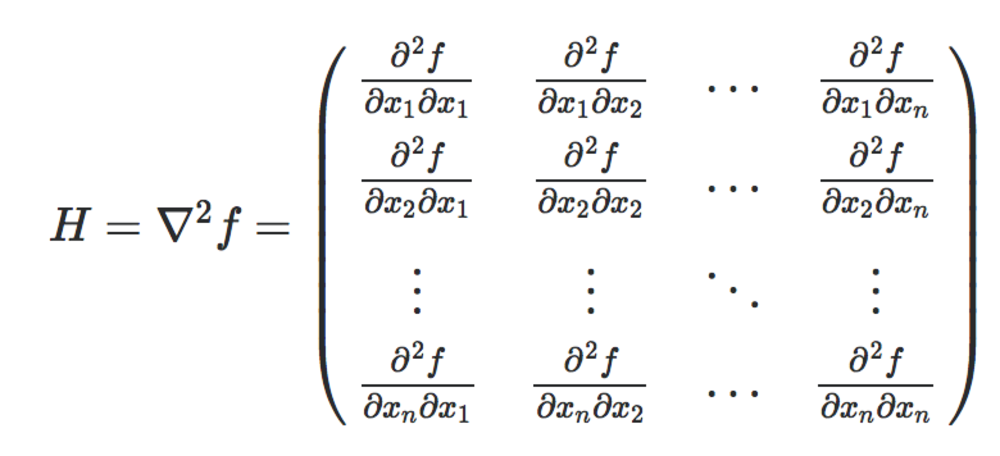
この章を学ぶ前に必要な知識
条件
- y=f(x_1, x_2, ... x_n)のような多変数を入力に1変数を出力する関数を微分
- 関数は二階微分できることが前提
効果
- 各変数で2階微分を行い行列とする
ポイント
- ヘッセ行列は、極値の判定やニュートン法等最適化などの近似、画像処理で用いられる
- 関数が連続であれば二階微分の順序は問われない
解 説
以下のような\(x_1 \dots x_n\)を入力としてyの一変数のみを出力する二階微分可能な\(f\)の関数に対して、
$$y=f(x_1, x_2, \dots, x_n)$$
以下のような二階微分の行列にしたものをヘッセ行列と言う.
$$\begin{eqnarray}
H= \nabla^2 f =\left(
\begin{array}{cccc}
\frac{ \partial^2 f }{ \partial x_1 \partial x_1} &
\frac{ \partial^2 f }{ \partial x_1 \partial x_2}
& \ldots &
\frac{ \partial^2 f }{ \partial x_1 \partial x_n} \\
\frac{ \partial^2 f }{ \partial x_2 \partial x_1} &
\frac{ \partial^2 f }{ \partial x_2 \partial x_2}
& \ldots &
\frac{ \partial^2 f }{ \partial x_2 \partial x_n} \\
\vdots & \vdots & \ddots & \vdots \\
\frac{ \partial^2 f }{ \partial x_n \partial x_1} &
\frac{ \partial^2 f }{ \partial x_n \partial x_2}
& \ldots &
\frac{ \partial^2 f }{ \partial x_n \partial x_n}
\end{array}
\right)
\end{eqnarray}
$$
各行列の要素は以下のように記述できる.
$$H_{i,j} = \frac{ \partial^2 f }{ \partial x_i \partial x_j}$$ | ヘッセ行列とは |
\(y=f(x_1, x_2, x_3)=x_1^2+ 4x_1x_2+3x_2+4x_3^3 + 8x_1x_3^2\)のような場合、ヘッセ行列の例えば要素(1,2)は以下のようになる.
$$\begin{eqnarray}
H_{1,2} &=& \frac{\partial^2 f}{\partial x_1 \partial x_2} \\
&=& \frac{\partial { (2x_1 + 4x_2)}} {\partial x_2}\\
&=& 4
\end{eqnarray}
$$
上記を各要素で行うと以下のようになる.
\begin{eqnarray}
H=
\left(
\begin{array}{ccc}
2 & 4 & 16x_3 \\
4 & 0 & 0 \\
16x_3 & 0 & 24x_3
\end{array}
\right)
\end{eqnarray} | ヘッセ行列の例 |
ヘッセ行列は関数fが二階微分できて連続のときに微分する順序はどちらでもよくなり、
すなわちHの行列要素(i,j)と(j,i)は等しい値になる.
対角要素が等しいので、そのときヘッセ行列は対称行列になる. | ヘッセ行列の特性 |
ヘッセ行列は以下のようなときに用いられる.
アプリケーション
・与えられた極値が極大値、極小値、鞍点なのかどうかを判定
・画像処理において特徴点の算出で用いられる
・ヘッセ行列の固有値の積は、その点における主曲率を示す
・ニュートン法等の最適化の近似で用いられる | ヘッセ行列の応用 |
この章を学んで新たに学べる
Comments


