-
 @ThothChildren
@ThothChildren
- 2018.7.7
- PV 428
ヤコビ行列
ー 概要 ー
多変数関数を入力として多変数ベクトルを出力する関数fを入力の変数で一回微分して行列に整理したものをヤコビ行列と呼ぶ.またヤコビ行列の行列式をヤコビアンと呼ぶ.ロボットの関節角を求める計算などの最適化計算などにおいて用いられる.
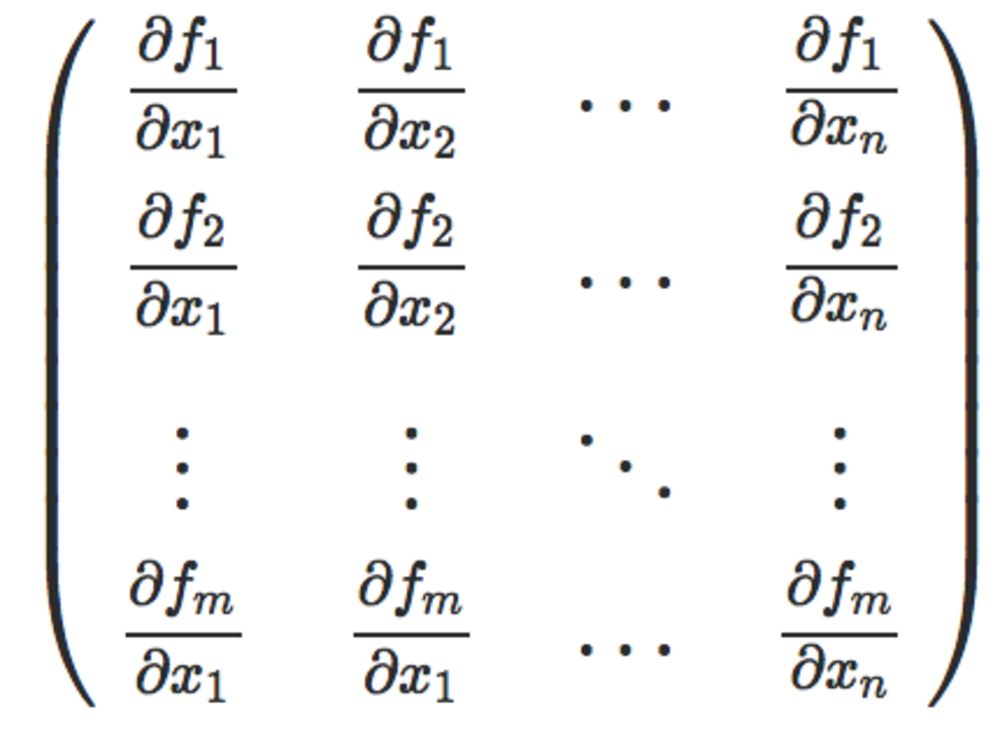
この章を学ぶ前に必要な知識
条件
- 多変数入力で多変数のベクトルを出力する関数
- 一階微分できる関数であること
効果
- 関数の一階微分した行列を得る
ポイント
- ある点xの線形近似をするときに用いる
- 上記の線形近似ができるため、最適化において勾配を求めるときに使用
- 例えばロボットの関節角を求めるときの最適化で用いられる
- ヤコビ行列が正方行列である点xの周りでヤコビ行列の行列式が0でないとき、微分可能な逆関数を持つと判定できる
- ヤコビ行列の行列式はヤコビアン
解 説
以下のような関数\(f\)の\(y_1,\dots, y_m\)を各\(x_1,\dots,x_n\)で微分して行列にしたものをヤコビ行列(またはヤコビアン)と呼ぶ.
$$f(x_1, x_2 ,\dots, x_n)=(y_1, y_2, \dots, y_m)$$
以下のように書ける.JaccobianからJと記述する.
$$\begin{eqnarray}
J = \left(
\begin{array}{cccc}
\frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} & \ldots & \frac{\partial f_1}{\partial x_n} \\
\frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} & \ldots & \frac{\partial f_2}{\partial x_n} \\
\vdots & \vdots & \ddots & \vdots \\
\frac{\partial f_m}{\partial x_1} & \frac{\partial f_m}{\partial x_2} & \ldots & \frac{\partial f_m}{\partial x_n}
\end{array}
\right)
\end{eqnarray}
$$
| ヤコビ行列
|
ヤコビ行列は関数\(\boldsymbol{f}\)の一階微分であるため、ある\(x_0\)の点の周りで以下のように線形近似したときに記述するときに利用できる.
$$\boldsymbol{ f }(\boldsymbol{x}) =\boldsymbol{f}(\boldsymbol{x_0})+\boldsymbol{J}(\boldsymbol{x_0})(\boldsymbol{x}-\boldsymbol{x_0}) + o(\boldsymbol{x^2} )$$
| ヤコビ行列について |
ヤコビ行列から幾らかわかることがあります.
1. 正方行列のヤコビ行列がある点において最大階数になっていない(階数が落ちている/退化している)とき、その点は臨界点
2. もしある点で行列式が0でないとき、その点の周辺で微分可能な陰関数があると判定可能. | ヤコビ行列の性質について |
ヤコビ行列は上記のようにある点における線形近似で勾配を与えるため、
関数の傾きを参考に関数の最小(最大)な点を求める最適化手法において、
用いられる.
ロボットの手先位置が決まっているときにロボットの関節角度を求めるような逆運動学でも使用される.
ロボットの関節角度をθとして、手先位置をxとすると、f(θ) = xと記述でき、ヤコビ行列Jを使いながら関節角度を求める.
| ヤコビ行列が使用される場面 |
3次元の\(x,y,z\)座標を極座標\(r,\theta, \phi \)を用いて記述できます.これのヤコビ行列を求めてみます.
$$
\begin{eqnarray}
x &=& rsin\theta cos\phi \\
y &=& rsin\theta sin\phi \\
z &=& rcos\theta
\end{eqnarray}
$$
と極座標で書ける時
$$
\begin{eqnarray}
J &=&
\left(
\begin{array}{rrr}
sin\theta cos\phi & r cos\theta cos\phi & -r sin\theta sin\phi \\
sin\theta sin\phi & r cos\theta sin\phi & r sin\theta cos\phi \\
cos\theta & -r sin\theta & 0
\end{array}
\right)
\\
det(J) &=& r^2 sin\theta
\end{eqnarray}
$$ | よく用いられる3次元極座標のヤコビ行列 |
この章を学んで新たに学べる
Comments


