-
 @ThothChildren
@ThothChildren
- 2018.7.17
- PV 2498
ヤコビ行列による逆運動学
ー 概要 ー
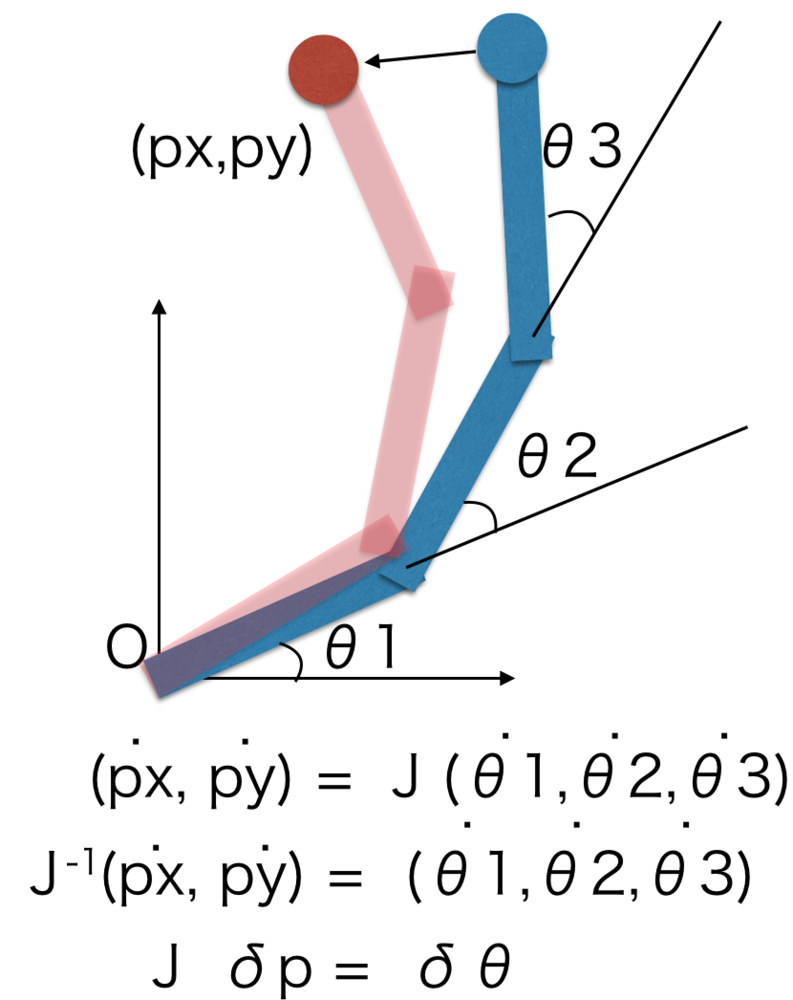
関節角度と手先位置のp=f(θ)の関係からδθ=J^-1()δp(Jはヤコビ行列)を導きこの勾配を利用して近似的に関節角を探索する方法についてまとめます.一般的に逆運動学は解析的に解けないため、このような繰り返し計算による解の導出を行います.ヤコビ行列による逆運動学はその中でも最も有名な手法です.
この章を学ぶ前に必要な知識
条件
- 関節角と手先位置の関係がp=f(θ)で書ける
効果
- 特定の位置に手先が来る関節角度が求まる
ポイント
- ヤコビアンが0にならないときのみ求まる
- 0のときは特異姿勢として解は求まらない
解 説
わかりやすい逆運動学 IK の解説動画 | |
関節角度\(\theta \)と手先位置\(p \)の\(p=f(\theta ) \)の関係から\(\delta \theta
= J^{-1}\delta p \)(Jはヤコビ行列)を導きこの勾配を利用して近似的に関節角を探索する方法についてまとめます.
一般的に3リンク以上で構成されるようなロボットは、逆運動学は解析的に解けないため、今回のような繰り返し計算による近似解の導出を行います.ヤコビ行列による逆運動学はその中でも最も有名な手法です.
ヤコビ行列を用いた逆運動学
1. \(\delta \theta = J^{-1}\delta p \)に基づいて\(\theta \)を更新.
2. 更新された\(\theta \)から順運動学によって求まる手先位置\(p_{new}\)を計算
3. 2.の手先位置が目的の手先位置\(p_{goal}\)との差分が誤差の閾値未満なら終了、そうでないなら1.から再度計算 | ヤコビ行列による逆運動学について |
解析的では求まらない式なのでNewton法による勾配を利用した解の探索を行っている. | ヤコビ行列による逆行列の繰り返し計算について |
関節角度\(\theta \)と手先位置\(p \)の関係は、ヤコビ行列\(J\)を使って
$$\dot{\theta} = J^{-1}\dot{p}$$
と表すことができる.
単位時間あたりではなく、微小変化同士の関係とする.
$$\delta \theta = J^{-1}\delta p $$
先のヤコビ行列による逆運動学の手順ではこの更新を\(\theta\)に加えて更新を行っていく.
$$\theta{ new} = \theta + \delta\theta $$
こうして得られた\(\theta\)から新しい手先位置座標は
$$p_{new} = f(\theta_{New})$$
と求められる. | 関節角度と手先位置の関係 |
ヤコビ行列\(J\)の行列式が0では、解は求まらない.
解が求まらないのは、ロボットのリンクが特殊な角度の状態になっていることや解が複数存在するためである.そのような逆運動学が求まらない姿勢を特異姿勢と呼ぶ.
ヤコビ行列の逆行列は\(\theta\)や\(p\)のランク数がどのようになっているかで求まるか求まらないかが変わってしまう.
そこで扱いやすくするために擬似逆行列を利用してヤコビ行列の逆行列を求めることが一般的である. | ヤコビ行列の注意点 |
擬似逆行列に関しては右のリンク先参照願います. | 擬似逆行列 |
この章を学んで新たに学べる
Comments
Reasons
知識: 擬似逆行列
次元が異なるなどして通常の逆行列を持たないが行列において似たような性質を持つ行列を擬似逆行列と呼ぶ.一般化逆行列またはムーアペンローズの擬似逆行列とも呼ぶ.ロボット工学の逆運動学などにおいて用いられる.


