©2024 Thoth Children All rights reserved.

深さ優先探索

ー 概要 ー

深さ優先探索はグラフデータの中でスタートのデータからとりあえずグラフの分岐がなくなるまで探索し、なくなったら少し戻って次の候補を探していく探索.データが深いところにありうる場合には幅優先探索でなくこちらを使用します.際限なく深くなりそうなときは最大深さを決めて途中で打ち切る場合もあります.通常幅優先探索より空間計算量ははるかに小さくなる.
Facebookシェア Twitterツイート LINEで送る このエントリーをはてなブックマークに追加
この章を学ぶ前に必要な知識
0
条件
  • データがグラフ状になっている
効果
  • データを深さを優先して探索する
ポイント
  • 頂点をV個、辺をE個があるとして、時間計算量はO(V+E)
  • 通常は空間計算量は幅優先探索より小さくなる
  • データが深いところにある場合は深さ優先探索を使うほうがよい
  • 空間計算量は、平均分岐数bと最大深さmでO(bm)
  • 今対応しているデータをメモするときは、LIFO(Last In First Out)のデータ構造で保持

解 説

深さ優先探索はグラフデータの中でスタートのデータからとりあえずグラフの分岐がなくなるまで探索し、なくなったら少し戻って次の候補を探していく探索. データが深いところにありうる場合には幅優先探索でなくこちらを使用します.膨大なデータを扱うときなどは、際限なく深くなりそうなときは最大深さを決めて途中で打ち切る場合もあります. 頂点がV個、辺がE個ある場合に、時間計算量はO(E+V)となる. 通常、幅優先探索より空間計算量は抑えることができ、平均分岐数bと最大深さmでO(bm)となる. 空間計算量を抑えることができるのは、今対応しているデータをメモするときに幾らか不要なものを除去することができるからである.このときデータはLIFO(Last In First Out)のデータ形式で持つ.
深さ優先探索について
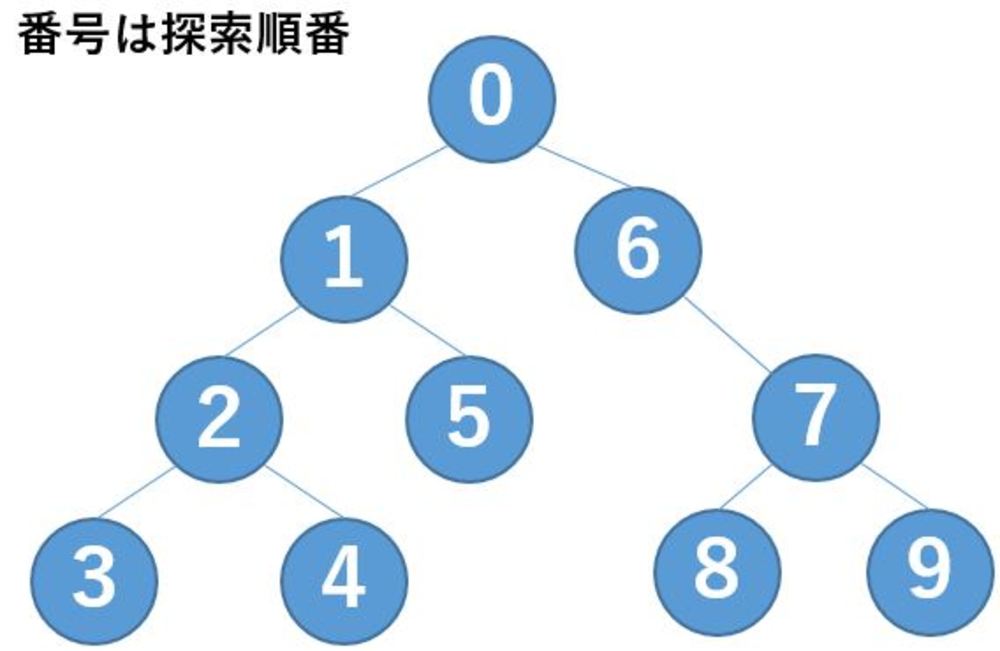
ノードの番号は探索する順番である. 最も深い3番に至るまでデータを展開していき、少しずつ戻っては次のノードを確認していく.
深さ優先探索で今処理中のものを保持している様子. 0,1,2を確認し目的のデータでなかった場合に、次は3を処理することになります.保持している3,4,5,6の先頭になっている3を取り出すためです. 3にももし子ノードがいれば新しくLIFOに加えますが、3は末端ノードのため特にノードには加えません.
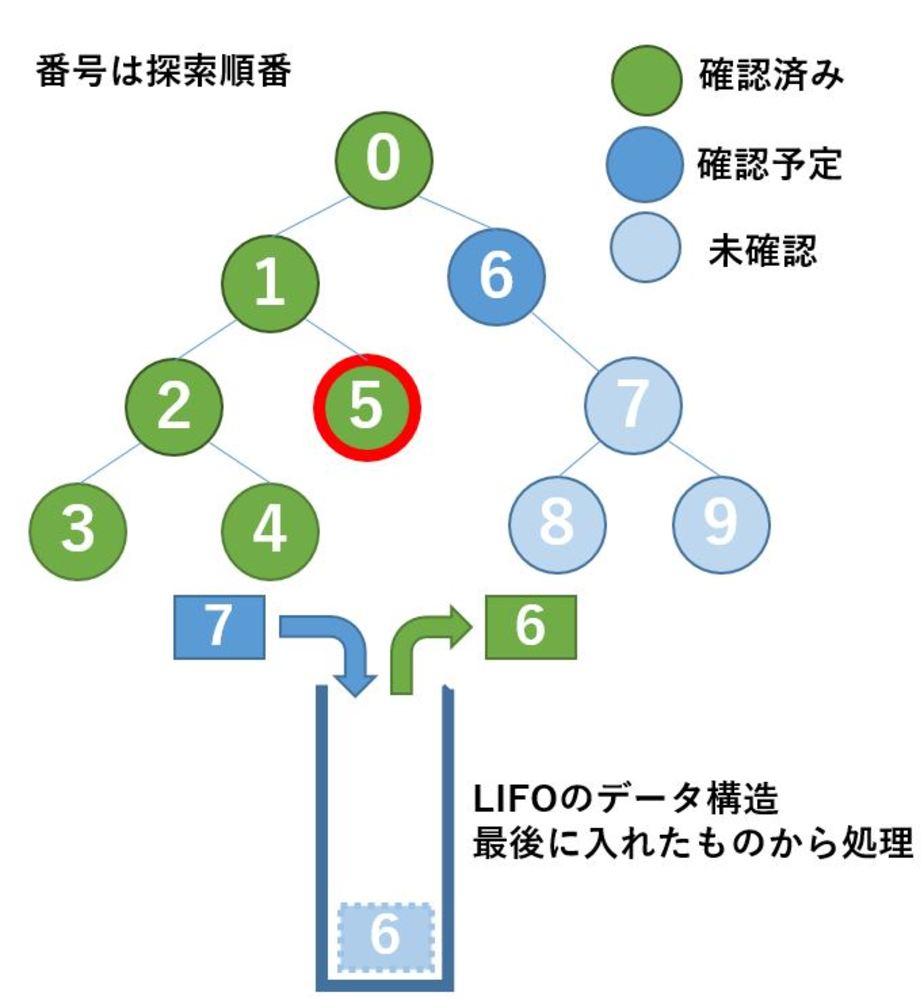さて3,4,5も確認して目的のデータ出なかったとします. 次にLIFOに入っているのは6のみなので、6を取り出します.しかし6には子ノードの7があるためこれをLIFOに入れることになります. 取り出した6を次に確認して次の処理に移ります.この後は7を取り出しますが、次の8と9を入れます.
この章を学んで新たに学べる
Comments

Reasons
>>隠す