-
 @ThothChildren
@ThothChildren
- 2018.8.8
- PV 347
ダイクストラ法
ー 概要 ー
ダイクストラ法は、負のコストがない回路において、ルートを選択を工夫して最短経路を見つけ出していくことで、ベルマンフォード法より効率的に探索することのできるアルゴリズム.普通の実装では計算量はO(n^2)だが、適当なヒープを用いることでO(E+nlog(n))になる.
この章を学ぶ前に必要な知識
条件
- 負のコストを含まないグラフ
効果
- グラフから最短経路を見つけ出す
- ベルマンフォート法より効率的.負のコストを含む場合のみベルマンフォート法.
ポイント
- 常にもっともコストの低いノードを処理する
解 説
ダイクストラ法は、負のコストがない回路において、ルートを選択を工夫して最短経路を見つけ出していくことで、ベルマンフォード法より効率的に探索することのできるアルゴリズム.
普通の実装では時間計算量はO(n^2)だが、適当なヒープを用いることで時間計算量はO(E+nlog(n))になる.
負のコストが経路になければダイクストラを使い、負のコストがあればベルマンフォードを使う.
ダイクストラ法
1. すべてのノードのコストを∞とする
2. 頂点のリストをキューに持っておく.
3. キューから最もコストの低いノードを取り出して、そこから隣接しているノードを更新する.更新したノードはどのノードから来たかを記録しておく.
4. キューが空っぽになるまで3を繰り返す. | ダイクストラ法とは |
ダイクストラ法で最小のコストとして選択したノードは
他のどのノードも自身のコストより高いため、スタート地点からそのノードまでの最小経路として確定できる. | ダイクストラの最小コストを選択したノードに関して |
1.ダイクストラの例 | |
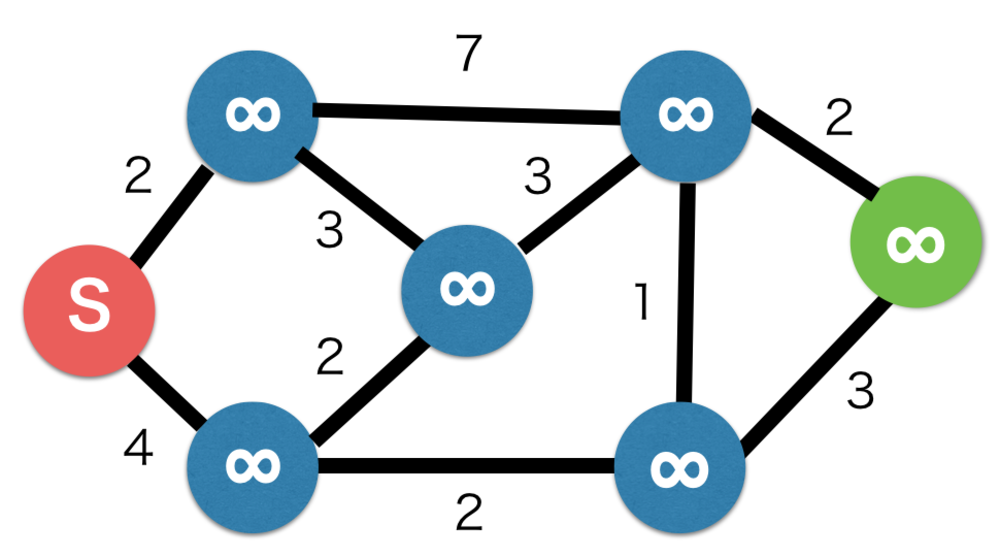 | すべてのノードのコストを無限で初期化する |
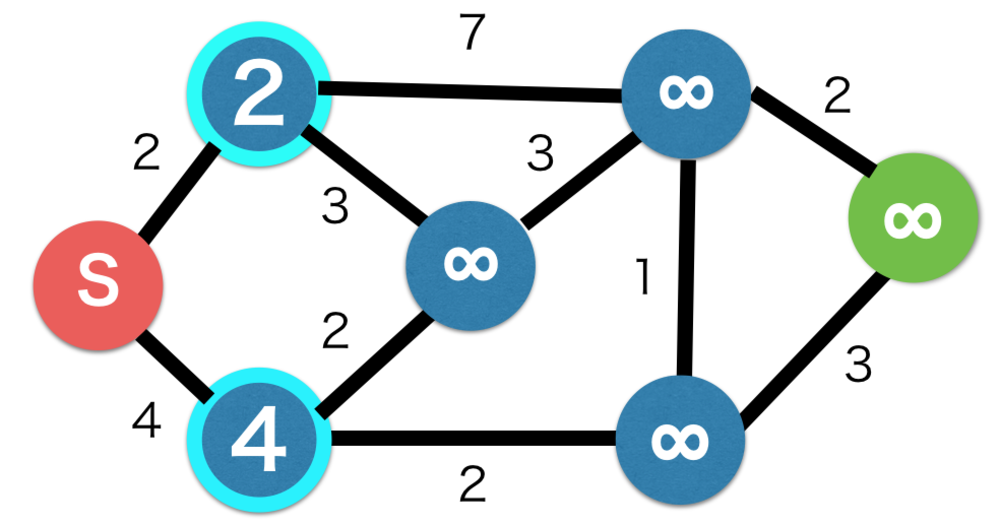 | 始めにスタート地点からエッジで接続しているノードを更新する |
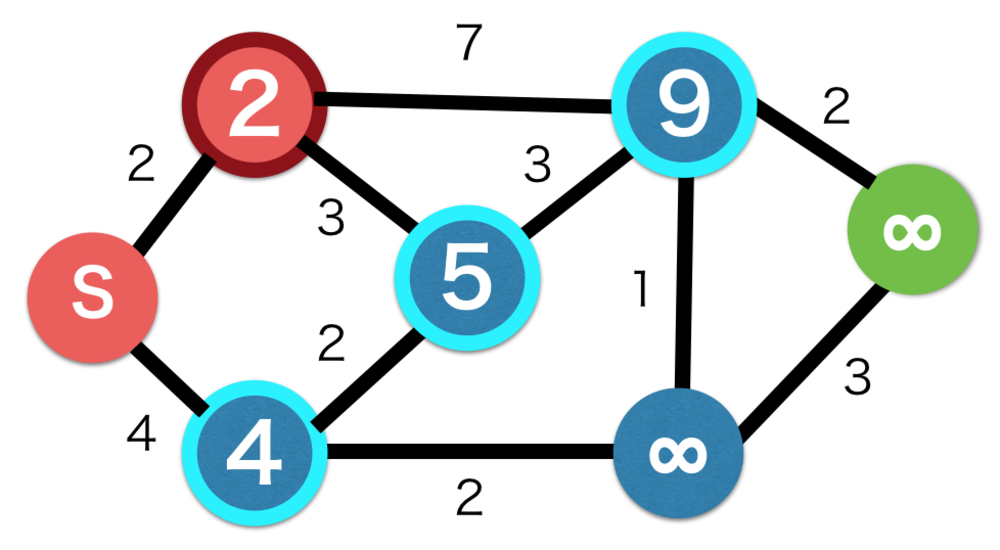
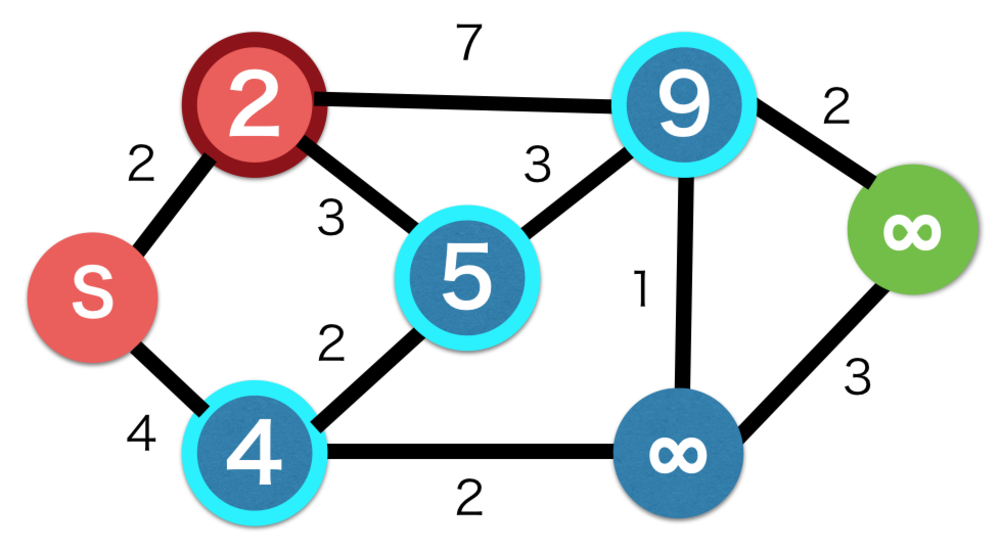 | 最もコストの低い2のノードに注目して隣接しているノードを更新する |
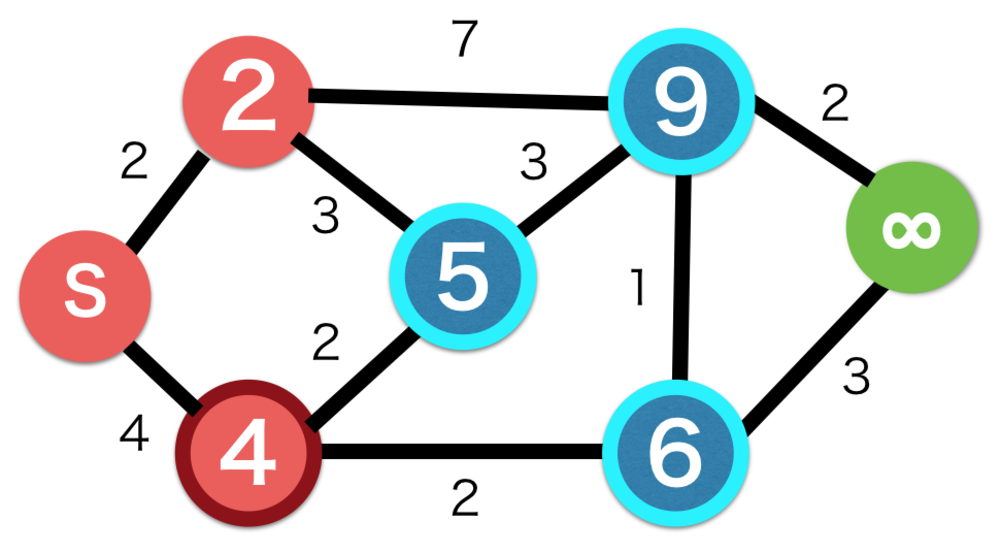 | 残るノードの中で最もコストの低い4のノードを選択する.隣接するノードのコストを更新. |
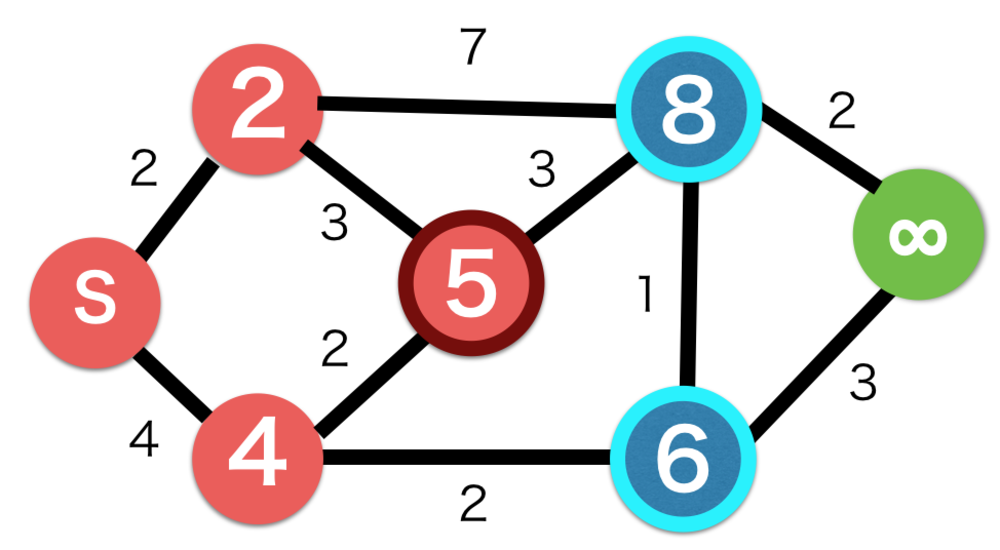 | 残るノードの中で最もコストの低い5のノードを選択.
隣接しているノードを更新する. |
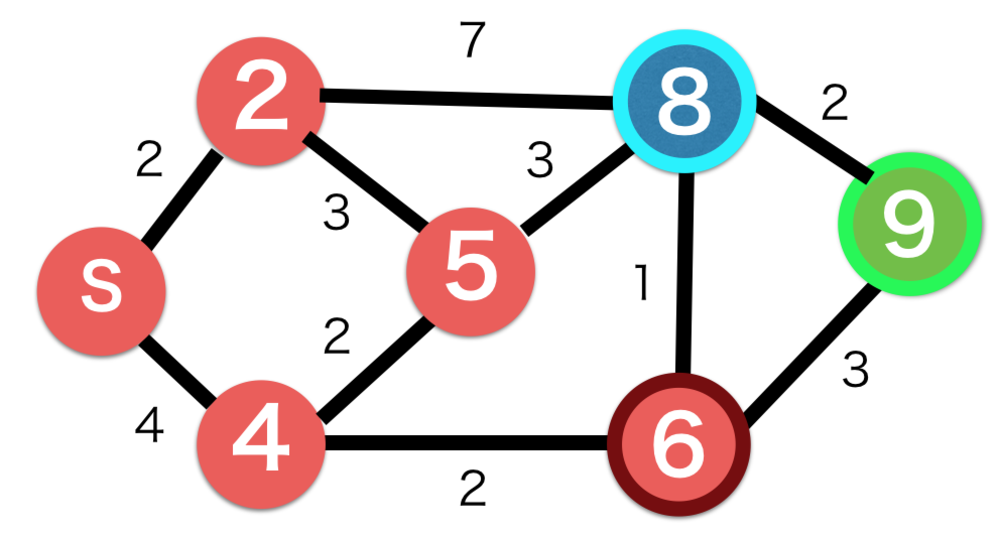 | 残るノードの中で最もコストの最小である6のノードを選択.
残りのノードを更新 |
この章を学んで新たに学べる
Comments


