©2024 Thoth Children All rights reserved.

極小極大値、最大最小値、局所大域とは

ー 概要 ー

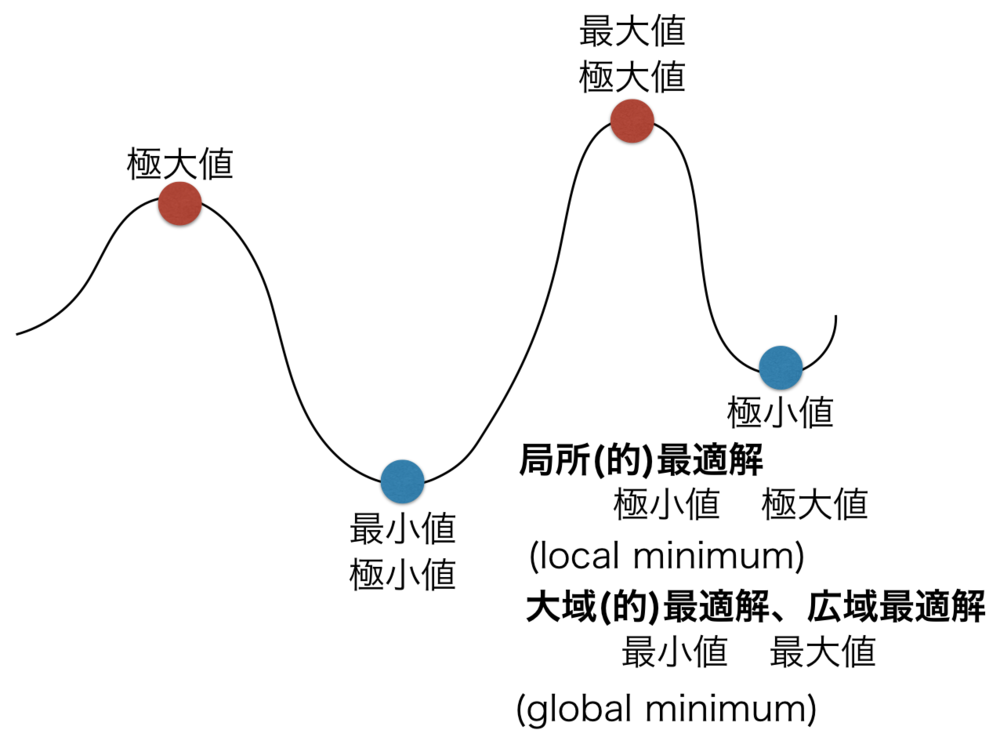
極小値、極大値、最大値、最小値、ローカルミニマム、と言った基本的なワードについてまとめておきます.最適化問題、機械学習、微積等で頻繁に使用される用語です.局所的なところにおいて最大である値を極大値、最小であるところを極小値(ローカルミニマム)と呼びこれらを最適化問題では局所最適解と呼ぶ.全体で最大となっているところを最大値、最小となっているところを最小値(グローバルミニマム)と呼びこれらを最適化問題では大域(的)最適解と呼ぶ.
Facebookシェア Twitterツイート LINEで送る このエントリーをはてなブックマークに追加
この章を学ぶ前に必要な知識
0
ポイント
  • 極大値や極小値はある関数において複数ある
  • 最大値は極大値であり最小値は極小値である.
  • 極大値や極小値はその近辺に置ける最大と最小の値
  • 最大値や最小値は全域における最大と最小の値
  • ローカルミニマムは極小値、グローバルミニマムは最小値を指す

解 説

極小値、極大値、最大値、最小値、ローカルミニマム、と言った基本的なワードについてまとめておきます. これらのワードは主に最適化問題、機械学習、微積等で頻繁に使用される用語です. 局所最適解 局所的なところにおいて最大である値:極大値 局所的なところにおいて最小である値:極小値(ローカルミニマム) 大域(的)最適解、広域最適解 全体で最大となっている値:最大値 全体で最小となっている値最小値(グローバルミニマム) 極小値や極大値は一つの関数の中に複数ありますが、その中に最大値や最小値も含まれます.
極小極大値、最大最小値、局所大域とは
この章を学んで新たに学べる
Comments

Reasons
>>隠す