ベクトルのなす角度

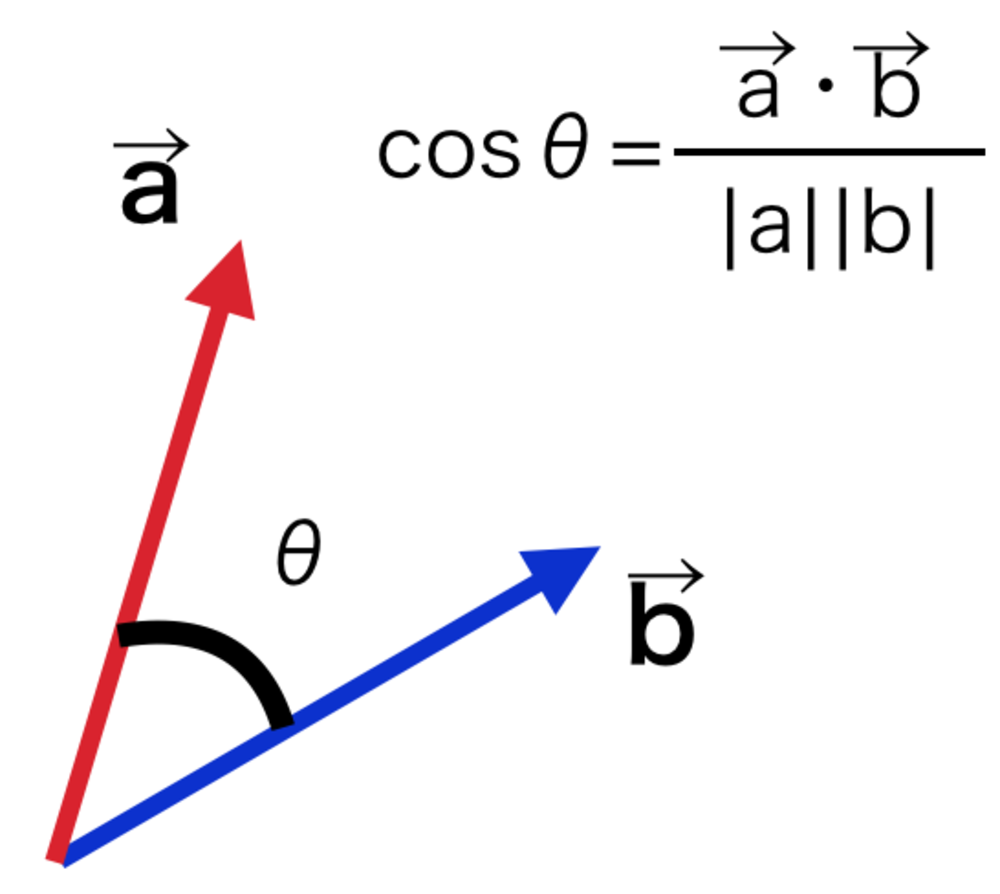
ベクトルは方向を示していますが、それらの方向の間にはどれくらいの角度があるのかを求めたいことがあります. どうやってベクトルとベクトルの間の角度を求めるか. ここで内積の式を思い出してみます.

$$\vec{a} \cdot \vec{b} = |\vec{a}||\vec{b}|cos\theta $$

内積の式は上のようにかけるのでした. このθは二つのベクトルの間のなしている角度を示しています.ちょうど今欲しかった値です. つまり、 θを求めたい ↓ cosθがわかれば、θはわかる ↓ 内積の公式から二つのベクトルの内積の値とベクトルの大きさがわかれば、 cosθが求まる といったようなことを導くことができます.

それでは実際に平面ベクトルでどのような計算をしてベクトルのなす角を求められるかを追ってみましょう. \(\vec{a}=(2,0)\),\(\vec{b}=(1,\sqrt{3})\)の場合を考えます. まずそれぞれのベクトルの大きさは、 $$|\vec{a}| = \sqrt{2^2 + 0^2} = 2$$ $$|\vec{b}| = \sqrt{1^2 + (\sqrt{3} )^2} = 2$$ また、内積は上の公式ではなく、各要素から以下のようにも求められます. $$\vec{a}\cdot\vec{b} = (2, 0 )\cdot (1, \sqrt{3}) = 2 \times 1 + 0 \times \sqrt{3} = 2$$ これであとは\(cos\theta\)を求めれば\(\theta\)が求まります. $$cos\theta = \frac{\vec{a}\cdot\vec{b} }{|\vec{a}||\vec{b}|} = \frac{2}{2\times 2} = \frac{1}{2}$$ となります. \(cos\theta\)がわかったのでこの場合\(\theta = 60^{\circ }\)とわかります.