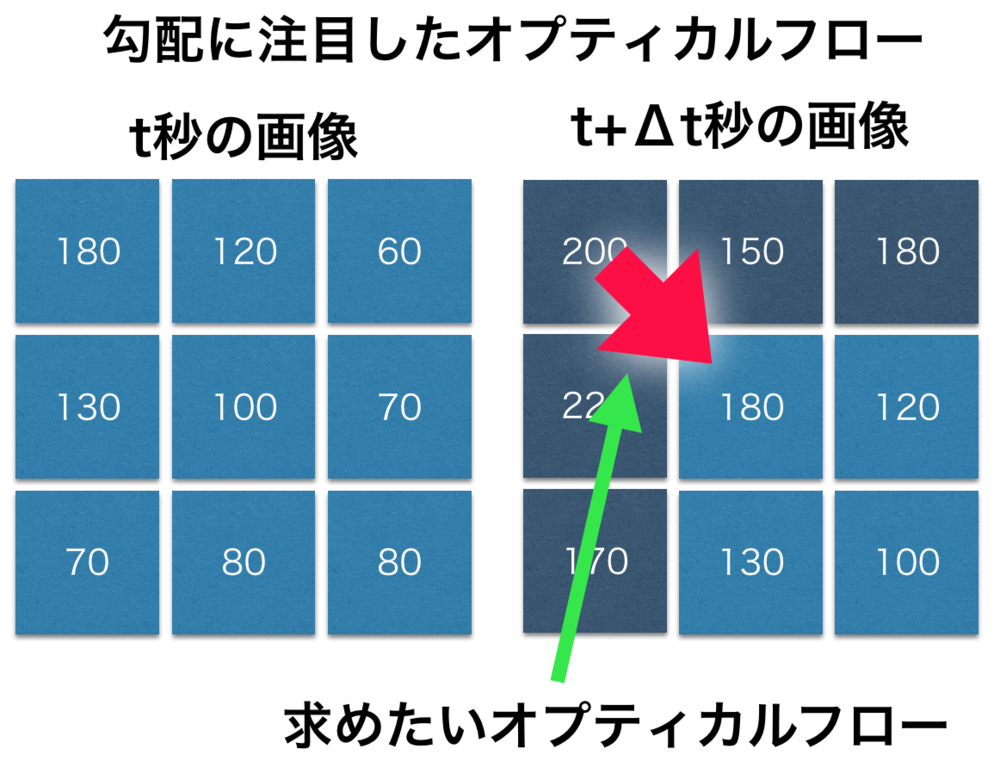
勾配に注目したオプティカルフロー

勾配に注目したオプティカルフローでは、複数あるオプティカルフローの算出方法のうち、画像の時間的空間的勾配に注目した算出方法. 複数の入力画像を使って、特徴的な点に注目してその点近辺でのオプティカルフローを求めます. そのため、オプティカルフローを求める手順は以下の通りです. 全体の手順 1. 追跡しやすい特徴的な点を画像から見つけ、トラッキングする対象とする 2. トラッキング対象としている点に対して「勾配法によるオプティカルフロー」を実行 → オプティカルフローが求まる. また、上記を求めるときに下記のような拘束条件を決めています. 前提条件 この手法を使うときには幾らかの前提条件を仮定します. ・微小な時間では移動する量も微小であること ・微小な時間では移動した先でも明るさが変わらないこと

オプティカルフローについては、リンクを参照してください.

下記の説明を理解する上で、「画像の一次微分」は知っておく必要があります.必要があれば参照ください.

それでは、詳細な処理についての説明に入ります. 数式が多いですが、簡単です. ほとんど同じだけど、わずかに時間に差がある二つの画像\(I_t, I_{t+\Delta t}\)があるとします.これはt秒でとったのと、\((t+\Delta t)\) 秒あとでとったあとの画像だと思ってください.\(\Delta t\) はすごく小さな時間です. 画像の特徴的な画素に注目します. \((x,y)\)という画素に注目したとしましょう. このとき、「\(t\)秒の時の\(I_t\)の\((x,y)\)」と「\(t+\Delta t\)秒の時の\(I_{t+\Delta t}\)の\((x+\Delta x,y+\Delta y)\)」が対応する同じ画素だったとすると以下の式が成り立ちます. $$I_t(x,y) = I_{t+\Delta t}(x+\Delta x, y+\Delta y)$$ と書くことができます.tも変数なので、一つの引数としてしまいましょう. $$I(x,y,t) = I(x+\Delta x, y+\Delta y,t+\Delta t)$$ このように書いても言いたいことは同じです.特に変わっていません. このとき、本当にどれも小さい変化しかしていないという仮定の元で以下のような近似をします.(頻出) $$I(x,y,t) = I(x,y,t) + \frac{\partial I}{\partial x}\Delta x + \frac{\partial I}{\partial y}\Delta y + \frac{\partial I}{\partial t}\Delta t +\dots $$ 小さい変化していないと言っているため、いつものように"\(\dots\)"以下は無視できます. そうすると共通の部分を除去して、以下のようになります. $$0 =\frac{\partial I}{\partial x}\Delta x + \frac{\partial I}{\partial y}\Delta y + \frac{\partial I}{\partial t}\Delta t $$ そして表記を他のサイトと同じように変えると $$0 =I_x\Delta x + I_y\Delta y + I_t\Delta t $$ のようになります.\(I_x, I_y\)はIのx方向微分とy方向微分です. 先ほど貼った画像の一次微分のリンク先に書いてある方法で求められます.要は1画素x方向ないしy方向に動いたらどれだけ値が変わるか?といういかにも微分的な計算です. また、\(I_t\)も同様に今度は時間方向への変化です.同じ画素に注目したときに前後の画像でどれくらい値が変わっているかを計算するものです. さらに整理するため、両辺を\(\Delta t\)で割ると $$0 =I_x \frac{\Delta x} {\Delta t} + I_y\frac{\Delta y} {\Delta t} + I_t\frac{\Delta t} {\Delta t} $$ のように求まります.もちろん最後の\(\frac{\Delta t}{\Delta t}\)は1ですので、 $$0 =I_x \frac{\Delta x} {\Delta t} + I_y\frac{\Delta y} {\Delta t} + I_t$$

$$0 =I_x \frac{\Delta x} {\Delta t} + I_y\frac{\Delta y} {\Delta t} + I_t$$ さて、上記の式が得られました. \(\frac{\Delta x} {\Delta t} ,\frac{\Delta y} {\Delta t} \)の意味はもちろん、微小時間がたったときにどれだけxまたはyが移動するかという意味になります.つまり、オプティカルフローとして求めたかった値になります. 先にも述べたように\(I_x, I_y, I_t\)は画像が複数枚あれば、ある点に注目して求めることができます. しかし、上記の式だけでは肝心の\(\frac{\Delta x} {\Delta t} ,\frac{\Delta y} {\Delta t} \)に関してはわからないままです.

上記までで一つの式が導けました. しかし、不定なパラメータがまだ二つあるため、これでは解が求まりません. そこで新しい拘束条件を加えて式を追加することで、解が解けるようにします. LucasKanade法やHorn–Schunck法がそのため導入されます.