©2024 Thoth Children All rights reserved.

トポロジカルソートのDAG経路探索

ー 概要 ー

有向非循環グラフ(DAG)の最短経路探索を線形時間で探索を行う手法として、トポロジカルソートによるものが挙げられます.一度しかノードもエッジも参照しないため、ソート自体もその後の最短経路探索も線形時間で探索が完了します.
Facebookシェア Twitterツイート LINEで送る このエントリーをはてなブックマークに追加
この章を学ぶ前に必要な知識
0
条件
  • 有向非循環グラフであること
  • スタートするノードを決めておく
  • 重みが負でも使用可能
効果
  • 有向非循環グラフ(DAG)の最短経路を線形時間で探索
ポイント
  • トポロジカルソートを用いて線形で見つけることが可能

解 説

有向非循環グラフ(DAG)の最短経路探索を線形時間で探索を行う手法として、トポロジカルソートによるものが挙げられます.一度しかノードもエッジも参照しないため、ソート自体もその後の最短経路探索も線形時間で探索が完了します.すなわち時間計算量はO(V+E). 手順は非常に簡単です。 アルゴリズム 1. まずグラフをもとにトポロジカルソートを行います.O(V+E) 2. スタートするノードのコストを0として他ノードを全て∞に設定します. 3. トポロジカルソートの順番に重みを更新していきます.以下あるノードuに注目した場合です.(O(V+E)) 3.1 トポロジカルソートで順番に取得したuのノードに注目 3.2 自身の重みにコストを足して、依存関係のあるノードのコストを更新します.ノードのコストが更新しようとしている値より大きい場合のみ更新します.
トポロジカルソートのDAG経路探索について
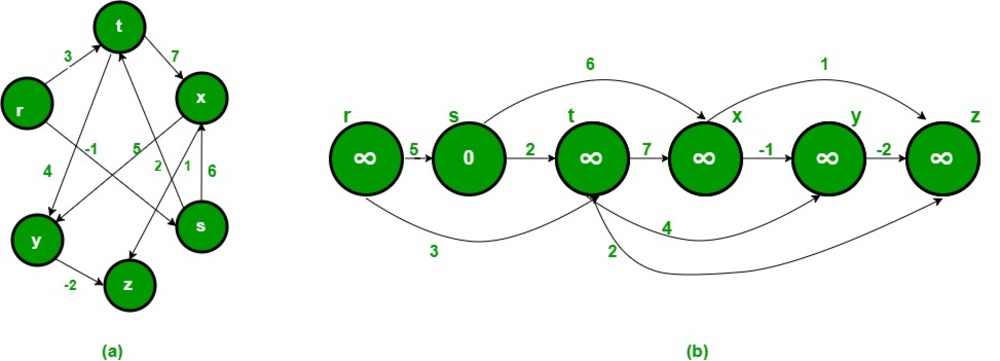左記画像はGeeksForGeeksより引用しています. まずトポロジカルソートを行い、 グラフ上から右側のソート列のように整形します. https://www.geeksforgeeks.org/shortest-path-for-directed-acyclic-graphs/ より引用
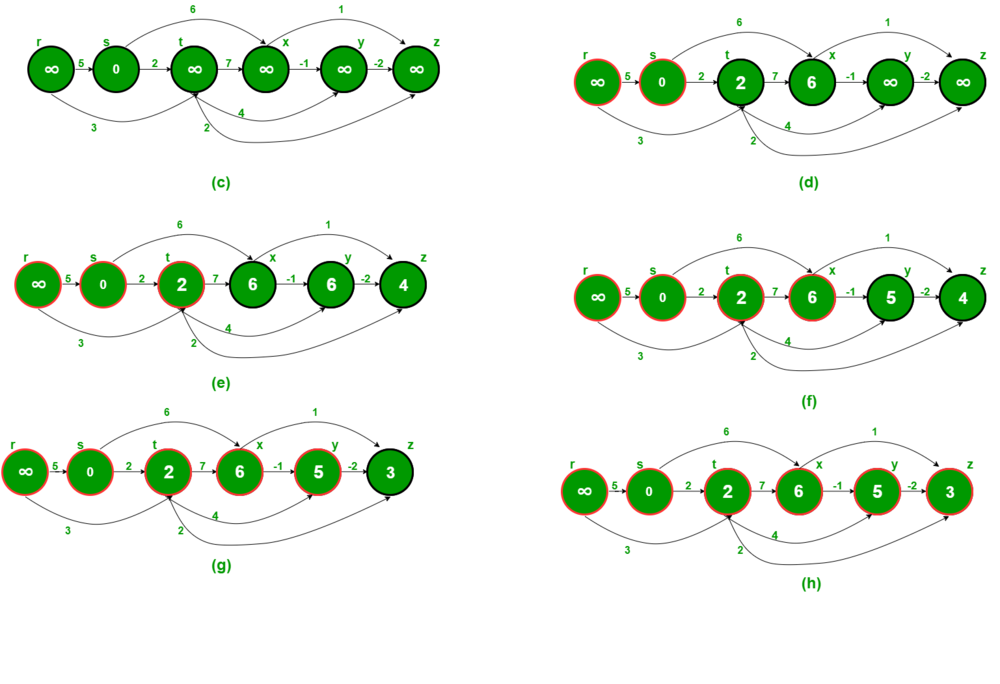
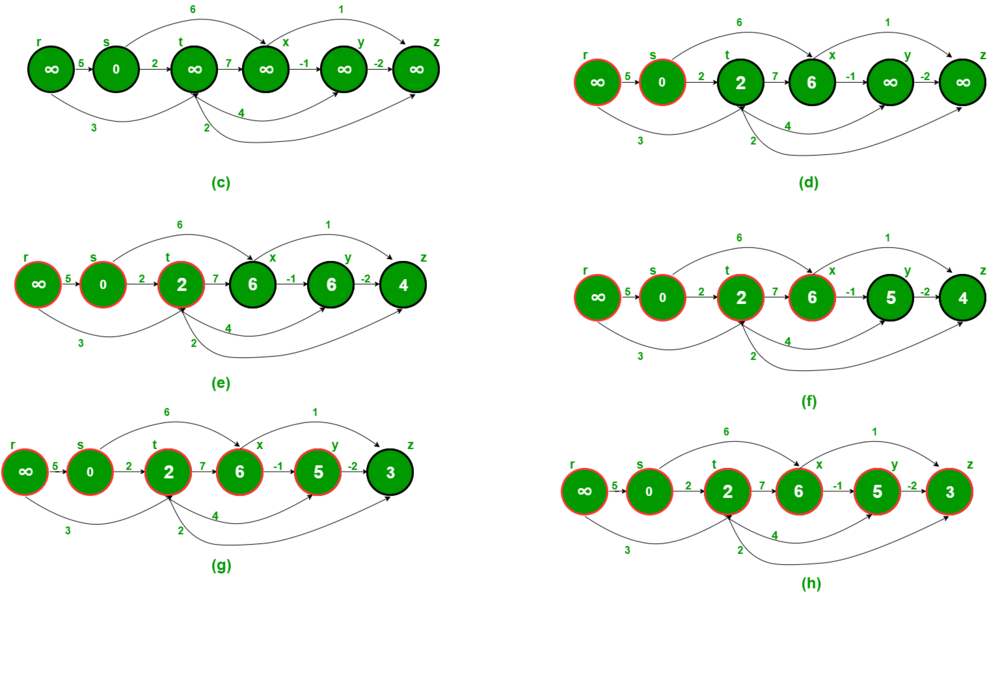こちらもGeekForGeeksより引用しています. さきほどトポロジカルソートしたノードに対してコストを記入していきます. トポロジカルソートの順番に更新していきます. https://www.geeksforgeeks.org/shortest-path-for-directed-acyclic-graphs/ より引用
この章を学んで新たに学べる
Comments

Reasons
>>隠す