-
 @ThothChildren
@ThothChildren
- 2018.10.26
- PV 5411
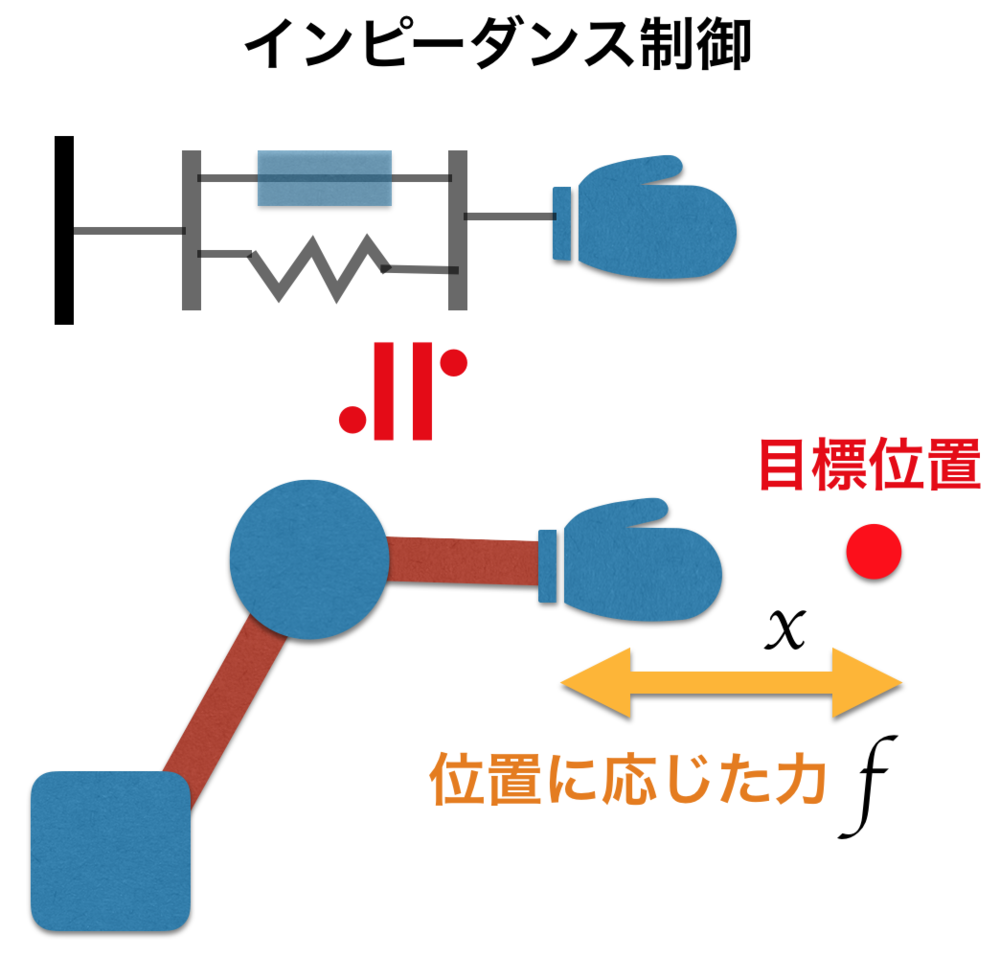
インピーダンス制御
ー 概要 ー
インピーダンス制御はバネマスダンパのモデルを元に仮想物体を想定してインピーダンスを制御する制御方法.力を特定の値に修正をするのみの直接力制御とは異なる間接力制御.外からの力の変化に対して緩やかに変化をする.接触制御.
この章を学ぶ前に必要な知識
条件
- 目標位置を設定
- 目標慣性行列M, 目標減衰係数行列D, 目標剛性行列K を決め、目標インピーダンスを決めとく
効果
- 環境の変化や外力を元に、バネマスダンパモデルに基づいた滑らか力制御を行う
- 外部から力がかかっても馴染むような力制御を行う.人と触れても安全.
ポイント
- 今どのような位置にあるかを入力に出力する力を決める力制御ベース
- どのような力が加えられているかから運動を決めるものはアドミッタンス制御、インピーダンス制御の逆
解 説
インピーダンス制御はバネマスダンパのモデルを元に仮想物体を想定してインピーダンスを制御する制御方法.
力を特定の値に修正をするのみの直接力制御とは異なる間接力制御.
外からの力の変化に対して緩やかに変化をする制御が可能となる.接触制御.
インピーダンス制御のメリット
・突然の外力や環境の変化があっても硬いままではなく、柔軟な動きをする
・人間と一緒に作業したときにも、人間に怪我をさせない | インピーダンス制御とは |
目標の(機械)インピーダンスが大きいと非常に強い力を出す動きとなり危険です.
インピーダンスが小さければ力により馴染むような動きになります. | 目標のインピーダンスの大小. |
1.インピーダンス制御(1自由度) | |
シンプルでわかりやすいため、まずインピーダンス制御(1次元)を考える.
ここで、もともと以下のようなモデルがあるとする.
$$m\ddot{x} + d\dot{x} + kx = F$$
これは既に環境にあるモデルでこれを以下のような\(u\)を加えてやることで、
$$m\ddot{x} + d\dot{x} + kx = F + u$$
以下のような好みのモデルにしてしまい、インピーダンスを調整することを目指す.(以下\(m_d, d_d, k_d\)はどれも理想的なインピーダンスのための目標値)
$$m_d\ddot{x} + d_d\dot{x} + k_dx = F$$
上記の場合は、システムで制御できるのは\(u\)だけで他は決まってしまっている値.
どんな\(u\)を与えればいいかは非常に簡単.
1) 力\(F\)がわかっている場合
\(F\)がわかっている場合は\(\ddot{x}\)が不要なため上記の式から除去するように引き算をする.
$$(d-\frac{m}{m_d}d_d)\dot{x} + (k-\frac{m}{m_d}k_d)x + (\frac{m}{m_d}-1)F= u$$
2) 力\(F\)がわからない場合
\(F\)がわからない場合は上記の式同士を引けば良い.
$$(m-m_d)\ddot{x} + (d-d_d)\dot{x} + (k-k_d)x = u$$
| インピーダンス制御(1次元)の式 |
2.アームのインピーダンス制御 | |
1次元ではなくアームのインピーダンス制御についての導出を行います.
今回も目標となるインピーダンスを出しつつ、外力も考慮してどのようなトルク\(\tau \)または力\(F_u\)を出すか決める流れになります.
目標のモデルは以下であるとする.
$$\boldsymbol{M_d\ddot{x}} + \boldsymbol{D_d(\dot{x} -\dot{x_d})}+\boldsymbol{K(x-x_d)} = \boldsymbol{F}$$
とする.ここで\(\boldsymbol{e}=\boldsymbol{\dot{x}} + \boldsymbol{x}\) とおけば
$$\boldsymbol{M_d\ddot{x}} + \boldsymbol{D_d\dot{e}}+\boldsymbol{Ke} = \boldsymbol{F}$$
と書ける.
次にマニピュレータの運動方程式を書く.直交座標系ではなく一般化座標\(q\)であることに注意.
$$\boldsymbol{M(q)}\ddot{q} +\boldsymbol{ \hat{h(q,\dot{q}})} = \boldsymbol{\tau}$$
ここで、\(\tau\)についてですが、これは外力\(\tau_F\)と今回加える駆動力\(\tau_u\)があるので、
$$\boldsymbol{M(q)}\ddot{q} +\boldsymbol{ \hat{h(q,\dot{q}})} = \boldsymbol{\tau_F}+\boldsymbol{\tau_u }$$
と書き直せます.
| 1次元ではなくアームのインピーダンス制御 |
$$\tau_F = J^TF$$
と書けるので、これらを上記の式に代入して
$$\boldsymbol{M(q)\ddot{q}} +\boldsymbol{h(q,\dot{q})} = \boldsymbol{J^TF}+\boldsymbol{\tau_u}$$
また
$$\boldsymbol{\dot{x}} =\boldsymbol{ J(q)\dot{q}}$$
であることや初めのモデルを使って\(\ddot{x}\)を表すなどすると
$$\tau = M(q)J^{-1}(q) M_d^{-1} (D_d\dot{e}+K_de)- M(q)J^{-1}(q) \dot{J(q)}\dot{q}+\hat{h(q, \dot{q})}+\\
(M(q)J^{-1}(q)M_d^{-1}-J^T)F$$
上記がインピーダンス制御を行うために必要なトルクとなる | インピーダンセス制御で与えるべきトルクτを求める |
 | インピーダンス制御の概念図 |
この章を学んで新たに学べる
Comments


