<<展開
©2024 Thoth Children All rights reserved.

ヒルベルトR-Tree

ー 概要 ー

ヒルベルトR-Treeは空間充填曲線であるヒルベルト曲線を用いてデータを順序づけしてより高速に効率的なデータ構造を作って高速化したR-Tree.ヒルベルト曲線は多次元を近いものを近いまま1次元に落とし込む曲線で今回の最小外接矩形の作成に寄与する.
Facebookシェア Twitterツイート LINEで送る このエントリーをはてなブックマークに追加
この章を学ぶ前に必要な知識
0
条件
  • 矩形情報や立方体情報などのデータが入力
効果
  • 空間での探索に特化しており多次元データを高速に探索するデータ構造
  • B-Treeを多次元にしたR-Treeを工夫して高速化したヒルベルトR-Tree
ポイント
  • 更新、削除、追加がほぼないならPacked hilbert R-tree
  • 更新、削除、追加が多いならDynamic Hilbert R-Tree
  • 如何に最小外接矩形をクラスタリングするかがR-Treeの効率化には大切でそれを工夫している
  • 空間充填曲線であるヒルベルト曲線は、高次元で近いものに一次元の近いインデックスを割り当てることができる

解 説

ヒルベルトR-Treeは空間充填曲線であるヒルベルト曲線を用いてデータを順序づけしてより高速に効率的なデータ構造を作って高速化したR-Tree. R-Treeでは如何に近い矩形データで効率的な最小外接矩形を作るかが高速化の鍵であった. ヒルベルト曲線は多次元データを近いものを近いまま1次元に落とし込む曲線で今回の最小外接矩形の作成に寄与し、検索効率を向上させている. 大きく二種類に分けることができる. Packed Hilbert R-Tree : データの更新、追加、削除が少ない時により効率的なデータ構造. 各矩形等に対してヒルベルト曲線によるインデックス付で得られるヒルベルト値を参考にデータ構造を構成していく. Dynamic Hilbert R-Tree : データの更新、追加、削除が多い時により効率的なデータ構造. Packed Hilbert R-Tree同様にヒルベルト曲線を用いてデータ構造を作成するが、分割時に工夫を行なっている.
ヒルベルトR-Treeとは
Dynamic Hilbert R-Treeの場合は、各ノードで最小外接矩形の値と、その中に含まれる最大ヒルベルト値と子ノードへのポインタを持っている.ヒルベルト値は各外接矩形の中心に対して求める. この木構造はR-TreeとB+-Treeのハイブリット版となっている.
Dynamic Hilbert R-Tree
R-Treeに関してはリンク先参照.
R-Tree
ヒルベルト曲線に関してはリンク先参照.
ヒルベルト曲線
この章を学んで新たに学べる
Comments

Reasons
>>隠す

知識: ヒルベルト曲線
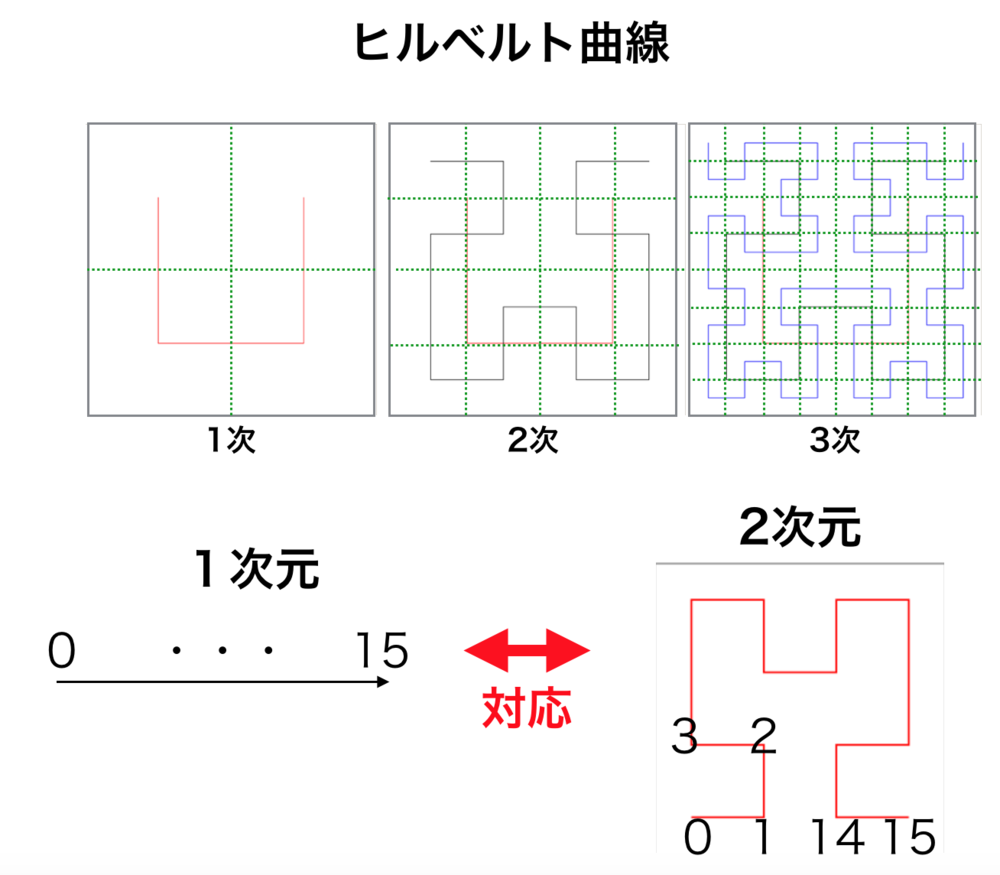
ヒルベルト曲線(Hilbert Curve)は、平面や空間内の単位正方形、単位立方体を特定のパターンに乗っ取って全て通るフラクタルな空間補充曲線の一つ.(一本の線で全部のブロックを通るようにする)他の空間充填曲線によってマッピングを行うよりもより位置関係を保持する曲線になっている.応用例も多く、空間インデックスや検索、などがある.1次元の値がn次元に対応しているため、原点からの距離が近いとその空間でも近いとわかる.
知識: R-Tree
R-Treeは空間インデックスなどに使用される空間データや矩形情報などの多次元データを扱うツリー型データ構造.矩形データを近いもので集めてそれらの最小外接矩形を親ノードとしてつなげていく.