-
 @ThothChildren
@ThothChildren
- 2018.11.7
- PV 279
プリム法
ー 概要 ー
プリム法は、最小全域木を求める貪欲法ベースで時間計算量がO(E+V log V)となる探索アルゴリズム.時間計算量は実装方法に依存する.特定の点から始めて常に繋がりうるエッジのうち最小のコストのエッジを選択することを繰り返す.
この章を学ぶ前に必要な知識
条件
- 負の経路を含まない
効果
- 重み付き連結グラフにおける最小全域木を探索
- 最適な実装ではO(E+V log V)
- 木であるため閉路が含まれない
ポイント
- 実装方法によって時間計算量が依存
- アルゴリズムは貪欲法でシンプル
解 説
プリム法は、最小全域木を求める貪欲法ベースで時間計算量がO(E+V log V)となる探索アルゴリズム.(最小全域木は、エッジに重みがついている連結グラフで全ての点を最小のコストで結ぶ木)
時間計算量は実装方法に依存する.
アルゴリズムは非常にシンプルで、
特定の点から始めて常に繋がりうるエッジのうち最小のコストのエッジを選択することを繰り返す.
アルゴリズム
適当に選んだ点を一つ含んだ頂点リストVと
初めは空であるエッジリストEを用意
1. 現在のVのリストの中から次に結ぶことのできる点vとエッジeから最小コストになるものを選択
2. vをVに追加
3. eをEに追加
4. 上記を全点が含まれるまで繰り返す. | プリム法とは |
上記の最小コストのエッジを選択し続けることで本当に全体においても最適になっているかは背理法で示すことができる.
仮にエッジの選択を誤っていてよりコストの少ない経路で結ばれているとすると、aとcは直接ではなく別の点を中継して経路で結ばれていることになります.しかしエッジに負の経路はなくaからc以外への経路は常にaからcのコストを上回るため、よりコストの少ない経路は存在できません.
そのためエッジの選択は正しいとわかります. | 最小コストのエッジの選択の正しさ |
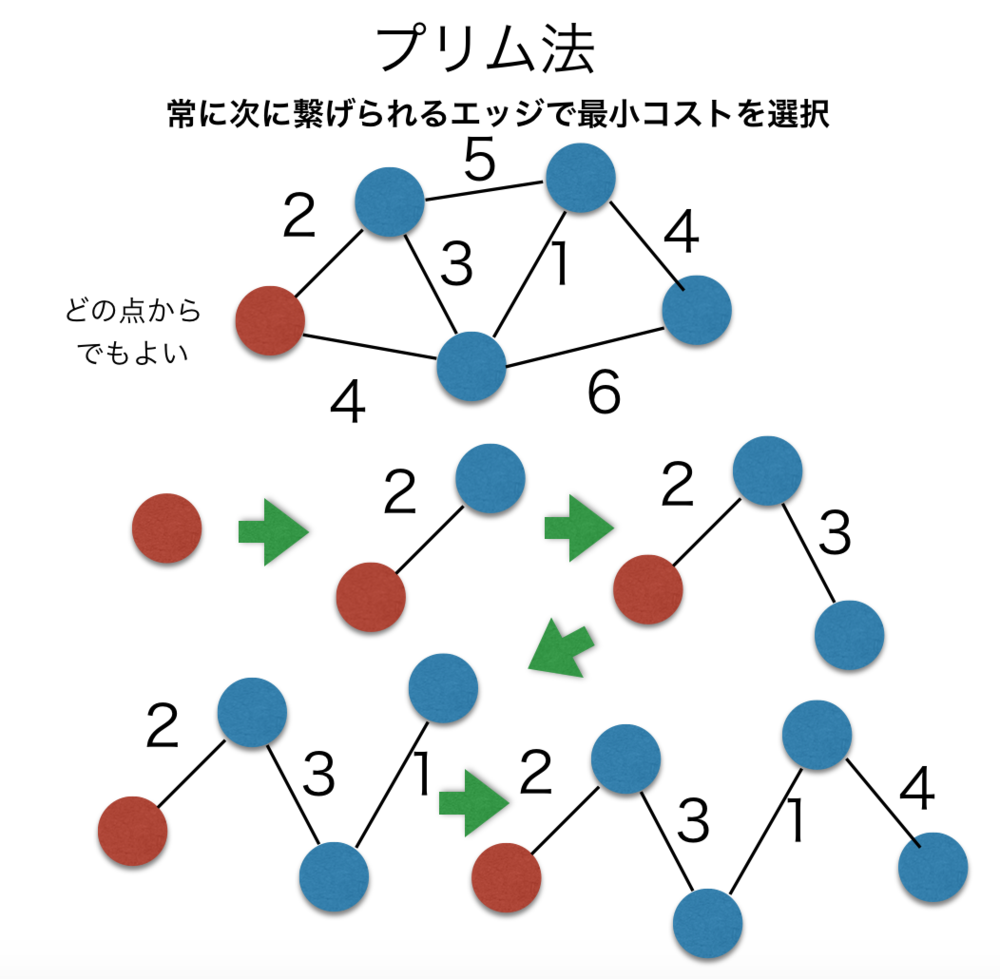
 | プリム法の概念図.
赤い点を開始点として常に繋げられるエッジのうち最小のええ時を選択をして繋げていく.
(2,4)の候補から2を選び
(3,5)の候補から3を選び
(5,1,6)の候補から1を選び
(6,4)の候補から4を選んでいる |
この章を学んで新たに学べる
Comments


