-
 @ThothChildren
@ThothChildren
- 2018.12.8
- PV 1555
CTC損失関数
ー 概要 ー
CTC Loss(損失関数) (Connectionist Temporal Classification)は、音声認識や時系列データにおいてよく用いられる損失関数で、最終層で出力される値から正解のデータ列になりうる確率を元に計算する損失関数.LSTMやRNNなどの出力を受けて正解文字列の確率を計算する.HMMのように前向き後ろ向きアルゴリズム、動的計画法を元に計算、微分可能であり誤差逆伝播が可能.
この章を学ぶ前に必要な知識
条件
- 入力は、時間区切りごとの文字や音素などの識別結果等
- 損失計算は正解ラベルの確率より求める
効果
- 時系列、画像、音声データなどから文字列等を抽出するネットワークの損失関数を定義
ポイント
- 正解ラベルとなる出力の全組み合わせの確率を算出
- HMMでも使用される前向き後ろ向きアルゴリズムによって確率を算出
- 微分可能で誤差逆伝播を行える
- LSTMやRNNの出力を受け付けて損失関数を計算
解 説
CTC Loss(損失関数) (Connectionist Temporal Classification)は、音声認識や時系列データにおいてよく用いられる損失関数で、最終層で出力される値から正解のデータ列になりうる確率を元に計算する損失関数.
LSTMやRNNなどの出力を受けて正解文字列の確率を計算する.LSTM等から渡されている入力は、音声データを時間単位で区切って認識している音素や文字列になっている.
確率の計算には、HMMのように前向き後ろ向きアルゴリズム(動的計画法の一種)を元に計算、微分可能であり誤差逆伝播が可能. | CTC Loss(損失関数) (Connectionist Temporal Classification)とは |
CTC損失関数は以下の関数で与えられる.\(x\)は最終的なラベル文字列等.("abc"や"おはよう"など)
$$Loss_{ctc} = -log(p(x))$$
上記誤差関数を最小化することは、すなわち\(p(x)\)の最大化にあたる. | CTC損失関数の定義 |
1.ネットワークの学習時 | |
CTC損失関数がわかっても計算する方法や実現手段が全く定かではない.
以下では音声または画像から文字列を認識する場合を想定して解説する.
LSTMの出力
まずLSTMの出力がどのような形式になっているかについて.
LSTMを出たときには、(多くの場合)時間ごとの文字の確率が得られる.
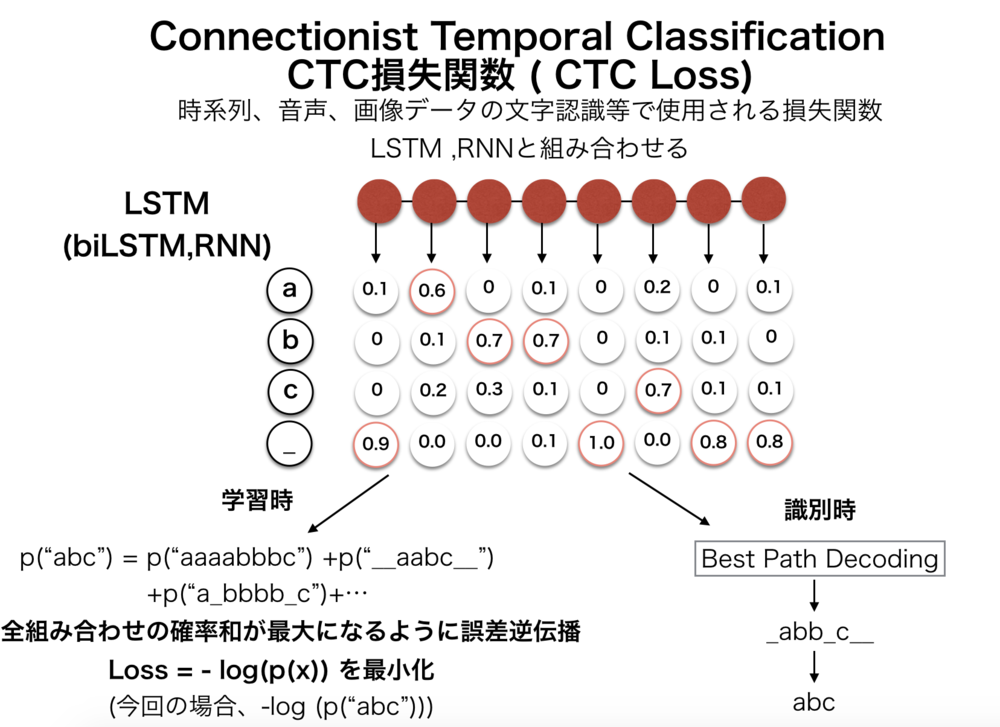
以下の画像のようにLSTM各ユニットから左から時間順序に沿って各時間での文字列の確率が与えられる.
また文字の他に特殊なブランク文字 _ が使用されている.これについてはあとで解説する. | CTC損失関数の学習時全体の流れ
(LSTMの出力) |
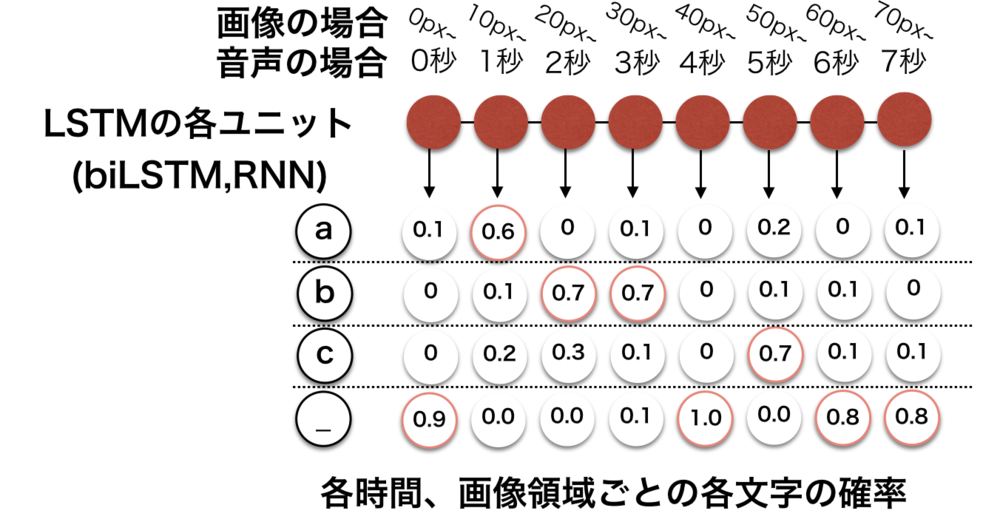 | LSTMの出力の状態の概念図.
各ユニットでは各文字列の確率を持っている |
学習時には正解文字列が常にわかっているので、例えば"abc"とする.
LSTMの出力からどのように正解文字列にするかというと、以下のルールに則って文字列を作る.
・同じ文字が連続した場合には、一つの文字にする.
・最後のブランク文字を全て削除する.
の二つのルール.
このルールに沿うと以下のように変換される.
ex)
_a_b__c_→abc, _aaaabc_→abc, b_o_oook→book, ___c_c_cccc_→ccc
ここで今回の文字列は"abc"だったとすると、LSTMのユニット数が8だったとすると,
_a_b__c_, _a_b_c___,aa_b_ccc_,abc_____も全てabcに変換される.
このような形にすることで例えば音声データの中で文字が伸びて発音されてしまった場合にも文字列を繰り返すことで表現して、正解文字列では消してしまえばいいだけになる. | CTC損失関数の学習時全体の流れ
(LSTMの出力から文字列生成) |
次に文字列の確率の計算を行う.
$$Loss = - log(p(x))$$
前述のように上記の確率\(p(x)\)をLSTMの出力を使って計算しなくてはならない.
さきほどの出力文字列からの正解文字列"abc"の求め方からわかるように\(p("abc")\)はLSTMの出力を使って以下のように計算される.
$$
p("abc") = p("abcccccc") + p("abbbbbbc") + p("aaaaaabc") \\
+ p("\_abbccc\_\_\_") + \cdots + + p("\_a\_b\_ccc\_\_\_")+p("\_\_\_\_\_\_abc")
$$
この全ての組み合わせの確率を足し合わせたものが、求めたかった\(p("abc")\)となる.
一つ一つの確率(例えば\(p("abc\_\_\_\_\_")\))の計算は容易.
LSTMの出力では"abc____"の確率が全て計算されているのでそれらを全て掛け合わせるだけ.
例えば
$$p("abc\_\_\_\_\_") = p_0("a")\cdot p_1("b")\cdot p_2("c")\cdot p_3("\_")\\ \cdot p_4("\_")\cdot p_5("\_")\cdot p_6("\_")\cdot p_7("\_")$$
ここで\(p_t()\)は時間ごと/ピクセルごとの確率変数.
あとは、こうして一つ一つ求めた確率を全パターンで足し合わせれば確率が求まる.
しかし、愚直に全ての計算を行うのは非効率であるため、確率は隠れマルコフモデル(HMM)でも使用される前向き後ろ向きアルゴリズム(動的計画法)によって計算される.
| CTC損失関数の学習時全体の流れ
(文字列の確率の計算) |
CTC損失関数は微分可能な関数のため、
通常通り誤差逆伝播計算を行うことが可能です.
長くなるため紹介しませんが、リンクを参照ください. | 外部リンク CTC詳細解説資料 |
2.ネットワークの識別時 | |
上記のようCTC損失関数を用いてネットワークを学習したあと、
識別時にはもちろんCTC損失関数は使用しないが、簡単に触れておく.
本来は、得られたLSTMの出力から最も確率p(x)が高くなるような文字列を前向き後ろ向きアルゴリズムから全て算出して推定すべきであるかもしれないが現実的ではない.
そこでBest Path Decodingが行われる.
近似解として、最もシンプルに各時間の確率最大の文字列を抽出してそれを正解文字列に変換する.
十分に学習されたネットワークにおいてはこのような近似でも十分に計算することが可能.
さきほどの画像に示した例の場合は、"_abb_c__"が出力となる.(それぞれの時間の最大値)
これは、"abc"に変換される. | ネットワークの識別時について |
この章を学んで新たに学べる
Comments


