刺激量と五感の感覚量のモデルが欲しい

人間の五感に外部から与えられる刺激量と人間の感じる感覚量の数学的モデルが欲しいときに有用なヴェーバーフェヒナーの法則を紹介します.外部からの強さは中程度であることを前提とします. ウェーバーの法則 初めにウェーバーの法則について簡単に触れます. ウェーバーの法則は人間が感じる差異の閾値が刺激量に比例することを示す法則です. $$\Delta S = S \times const $$ のように刺激量が大きいほど「人間が違いを感じる変化量の閾値」も大きくなります. 刺激が大きいと違いを感じる変化量の閾値が変わるというのは、つまり持っている荷物が大きい(思い)ほど、何か別の重りを加えた時にその全体の重量の差に気づくための閾値も大きくなる(つまりどんどん気づきにくくなる)ということ. フェヒナーの法則 フェヒナーの法則はウェーバーの法則(ウェーバー拘束 : Weber Const)を元に積分を行なったものになります. 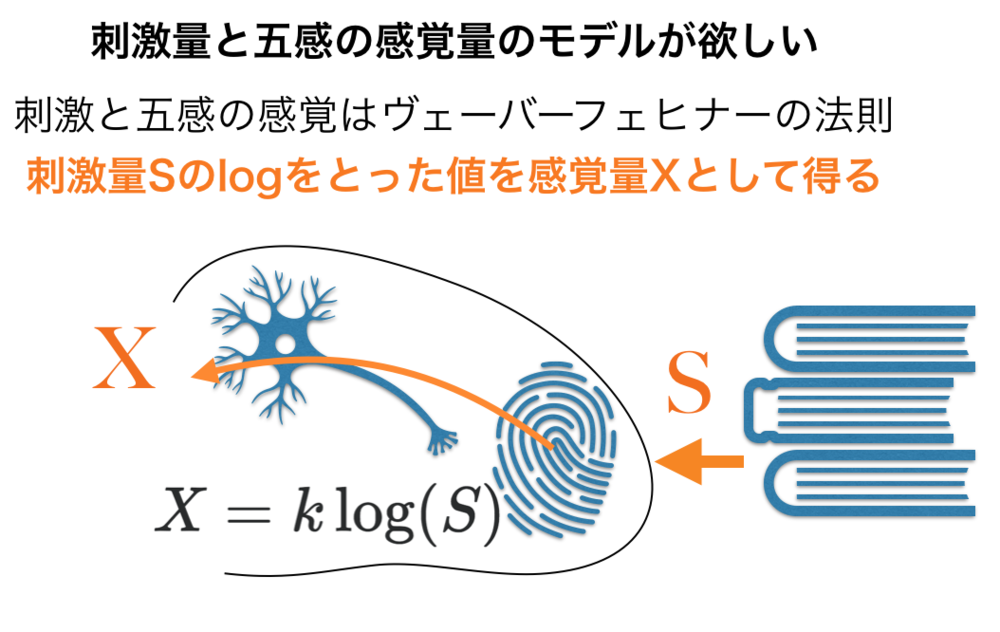この式の示すところは、ある刺激\(S\)が五感に与えらた時に感覚Xとしてはどの程伝わるかです. $$X = k\log(S)$$ 式の通りログスケールな値が感覚量として伝わることになります. たとえば、\(S=100\)が\(S=200\)に変化する時\(\Delta X=k\log(200) - k\log(100) = k\log(2)\)の感覚の差が得られます. 仮に\(S=200\)から始まった場合、上記と同じ量\(k\log(2)\)の感覚の変化を得られるには \(\Delta X=k\log(400) - k\log(200) = k\log(2)\)になるよう\(Z=400\)の力が与えられる必要があります. 上記の式は五感のどれにおいても中程度の刺激では近似的に成立します

人間の目の明るさに対する反応や重さを感じる反応については上記の式がよく当てはまります. ただ、音の大きさに関する知覚などには当てはめることができない.