-
 @ThothChildren
@ThothChildren
- 2019.3.3
- PV 299
Bairstow法による求根
ー 概要 ー
Bairstow法は、1次元多項式に対して効率的に全ての解を求める求根アルゴリズム.二次式の解を求めて関数を割るのを低次の式になるまで繰り返す手法.数値的な性質はよくなく桁落ちしやすいとされる.
この章を学ぶ前に必要な知識
条件
- 一変数一次元多項式f(x)が対象
効果
- 一次元多項式のすべての解を得られる
ポイント
- 数値的な性質はよくなく桁落ちしやすいとされる
- 多項式f(x)を割り切れるような二次式の係数を繰り返し求めて全ての解を計算
解 説
この章を学んで新たに学べる
Comments
Reasons
知識: ニュートン法による求根
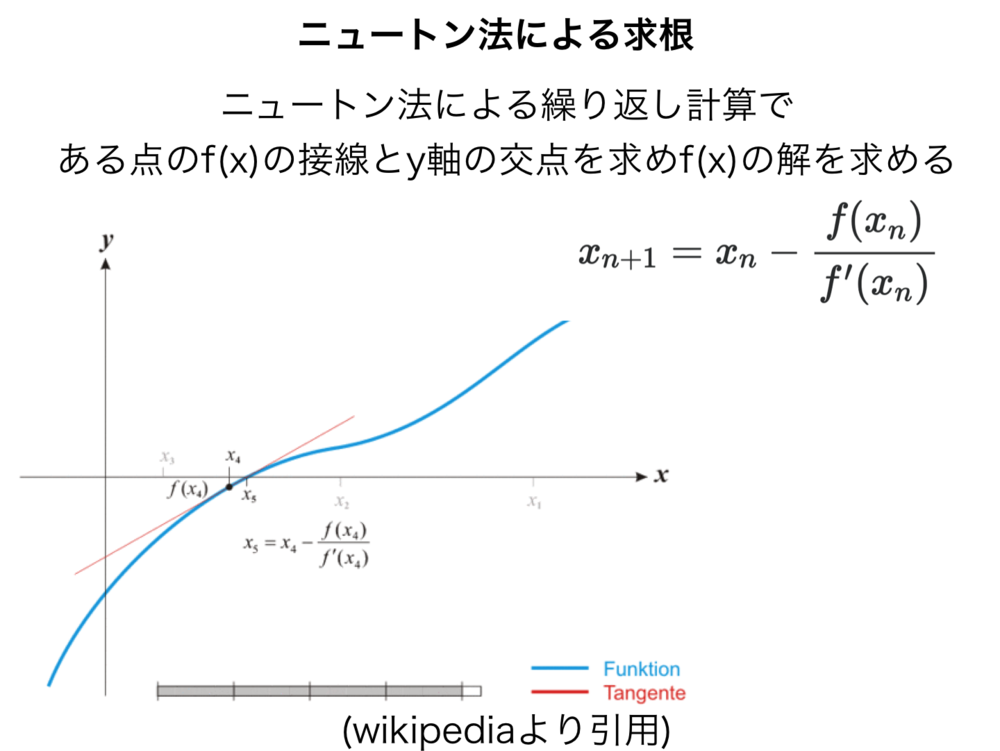
求根アルゴリズムとして有名である頻繁に使用されるニュートン法(1次元の場合)について紹介します.ニュートン法によって関数の値がゼロになる値等を算出します.探索する初期値に依存し、解は一つしか見つけられませんが、比較的高速です.導関数が適切に得られる必要があります.


