-
 @ThothChildren
@ThothChildren
- 2022.10.11
- PV 262
隠れマルコフモデル
ー 概要 ー
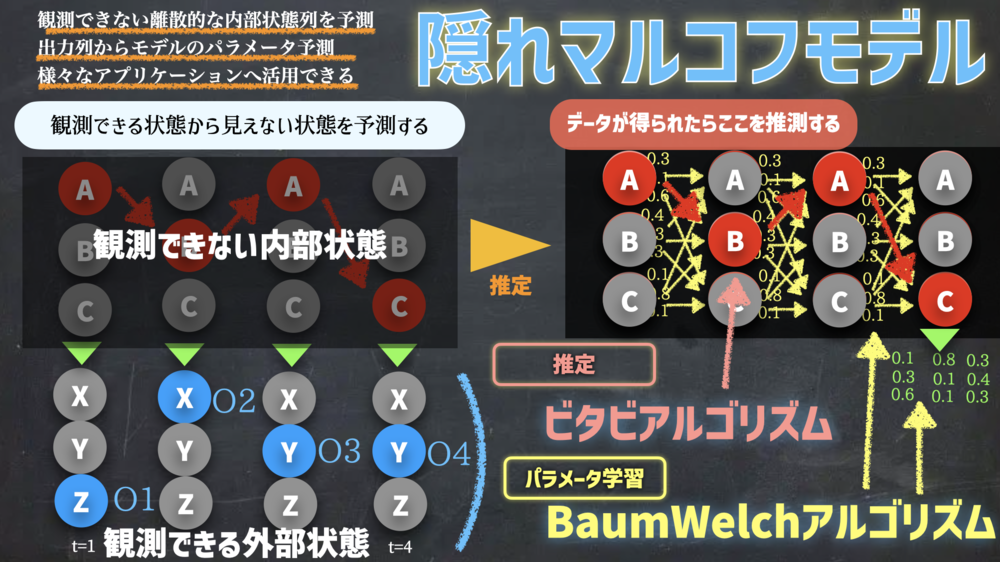
隠れマルコフモデル(HMM, Hidden Markov Model)は、内部の観測できない状態を外部で観測できる状態から推定する技術. 内部の状態は確率でどれかの状態に遷移し、遷移した先で決まった確率で観測される状態を出力する.ビタビアルゴリズムで内部の最も考えられる状態遷移を予測し、Forward-Barckwardアルゴリズムで各時刻、各状態の確率を算出し、BaumWelchアルゴリズムでそもそもモデルのパラメータを推定する.
この章を学ぶ前に必要な知識
条件
- 観測できない内部の状態と観測できる状態あり
- 観測できる状態は内部の状態によって確率で状態が定まる
- 内部の状態遷移の確率も外部の状態の確率も一定
- 離散的な状態を扱う
効果
- 観測された状態列から内部の状態列を推定
- 観測された状態列からモデルのパラメータを推定
- 音声データから文字列を起こすアプリや画像から人間の動作を読み取るアプリなど
- さまざまなアプリケーションに適用可能
ポイント
- モデルのパラメータλは遷移確率aと出力確率b
- パラメータλと観測されたデータから内部の状態を推定するビタアルゴリズム(Viterbi Algorythm)
- パラメータλと観測されたデータから各時刻各状態の確率を推定するForward-Backwardアルゴリズム
- Forward/Backwardは前向き確率と後向き確率を算出
- 観測されたデータから内部のパラメータλを推定するBaumWelchアルゴリズム)
- BaumWelchアルゴリズムはEMアルゴリズムの逐次的処理となっている
- マルコフ性を仮定するため、これまでの状態列を考慮した判断ができない
解 説
隠れマルコフモデルのわかりやすい解説
【数分解説】隠れマルコフモデル HMM: 観測情報から見えない離散的な内部状態の遷移を推定する手法. ビタビアルゴリズム,Forward-Backwardアルゴリズム,BaumWelchを徹底理解
| |||||||||
1.隠れマルコフモデルが想定する状況 | |||||||||
 | 隠れマルコフモデルの概要 | ||||||||
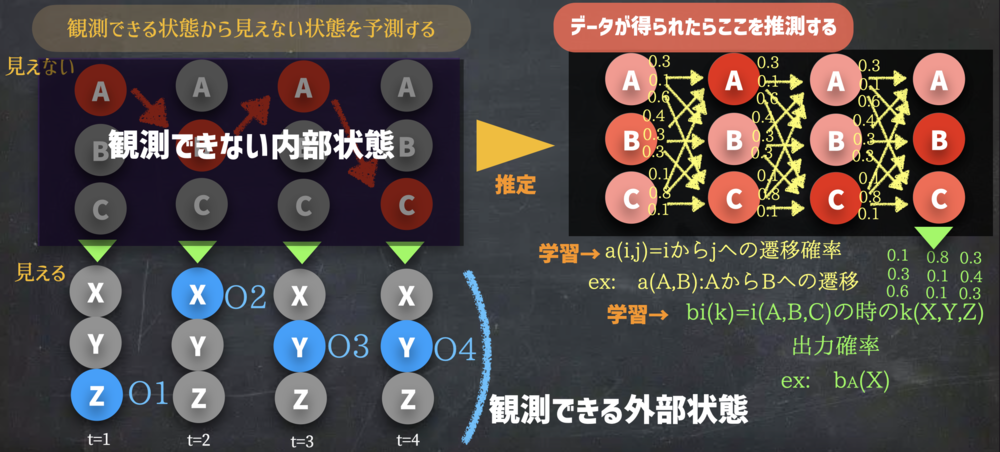
隠れマルコフモデルは下記を想定した問題を扱います
・観測できない内部の状態とそれに影響を受けて観測できる外部の状態
ex) 音声データ(観測できる)と表現する文字(観測できない:意味が直接はわからない)
画像データ(観測できる)と歩く/走る/座る動作の分類(観測できない:意味が直接はわからない)
・内部状態は常に一定の確率に従って、他の状態またはそのままの状態になる
ex) A,B,CがあったらA→A,B,Cのそれぞれに0.1,0.3,0.6で遷移.B→A,B,Cはまた別
・内部の状態に応じて外部で見れる状態はそれぞれの出力確率で決まる
ex) Aの時、外部ではX,Y,Zが出力される確率が0.3, 0.5, 0.2. と定まっている. BやCもそれぞれ
・時間は離散的にt=0~Tまで進む.それぞれの状態は時間ごとに定まっている
| 隠れマルコフモデルの対象とする前提 | ||||||||
 | 確率を含めて各変数のまとめ | ||||||||
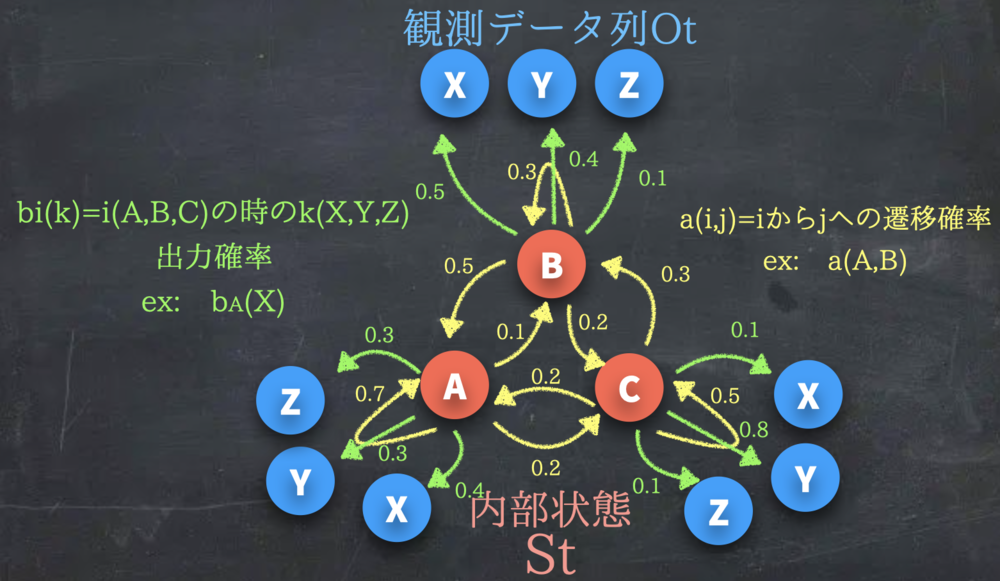
観測データ列をOとして\(t=0\) から\(t=T\)までの\(O_0~O_T \) O0~OTのデータがあるものとする.
内部の状態列をSとしてt=0からt=TまでのS0~STと呼ぶものとする.
内部状態間で状態iから状態jへの遷移確率は\(a_{ij}\) とする.
ある内部状態iで外部状態kを出力確率は\(b_i(k)\) とする.
パラメータ\(\lambda\)は\(a_{ij}\)と\(b_i(k)\)を合わせたものをさす. | 変数の前提 | ||||||||
隠れマルコフモデルは3つの問題とそれらを解決する手法があります.
以下ではそれぞれを解説していきます. | 3つの問題と各アルゴリズム
この後わかりやすく解説. | ||||||||
2.観測データとパラメータλで内部の最適な状態を推定 | |||||||||
2.1.愚直に推定する場合 | |||||||||
 | シンプルに最もあり得そうな状態をそれぞれ選択する場合 | ||||||||
観測された状態\(O_o\)~\(O_T\)をもとに内部の最も考えられる状態\(S_0\)~\(S_T\)がどれなのかをそれぞれの時刻t毎に決めていく必要があります.
例えば、t=5の時に\(S_0\)で確率0.2,\(S_1\)で確率0.5, \(S_2\)で確率0.3なら、\(S_1\)で決まりです.
しかし、t時間毎にそれぞれの状態の確率を比較して解が得られても一つ手前の状態とその後の状態を考慮できていません.
即ち絶対にあり得ないような遷移なども許容してしまいます.
それを避けるために、あり得る内部の状態遷移列を生成するようにするのがビタビアルゴリズムです. | 愚直に見つける | ||||||||
2.2.ビタビアルゴリズムで推定する場合 | |||||||||
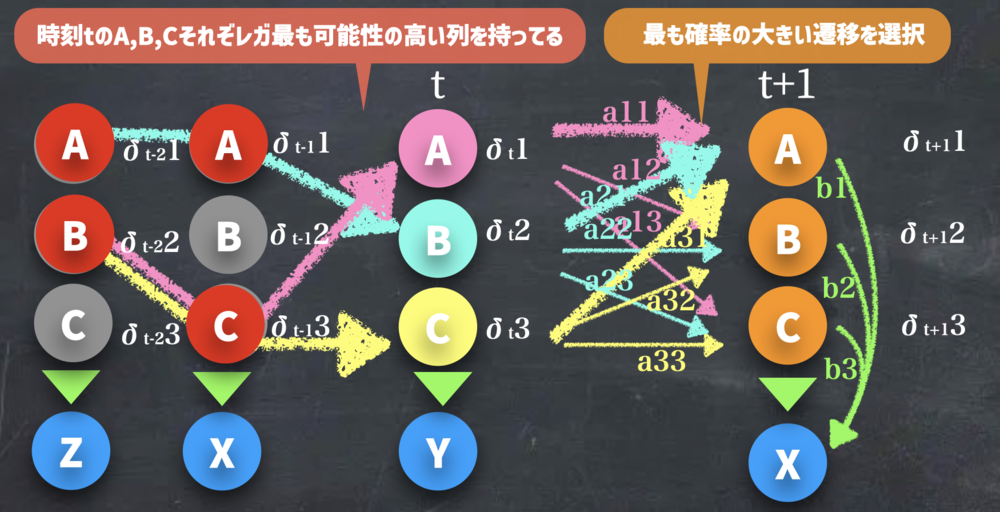 | ビタビアルゴリズムが
δt+1をδtで更新する様子.
tではそれぞれの状態がこれまで最も良かった経路を持っている | ||||||||
ビタビアルゴリズムでは、t=0からt=Tまで一つずつtを進めながら、
最も観測データが生成される確率が高い状態列を求めます.
t=0から常にそのtで最も確率が高い状態列を選んで遷移していけば、最も良い状態列は求まりそうです.
各tの各状態Sでは下記二つの状態を持つことになります.
・0からあるtまで遷移した時、観測データ列が生成される確率
・上記を再現するためにどこから遷移してきたかの情報
| ビタビアルゴリズムの概要 | ||||||||
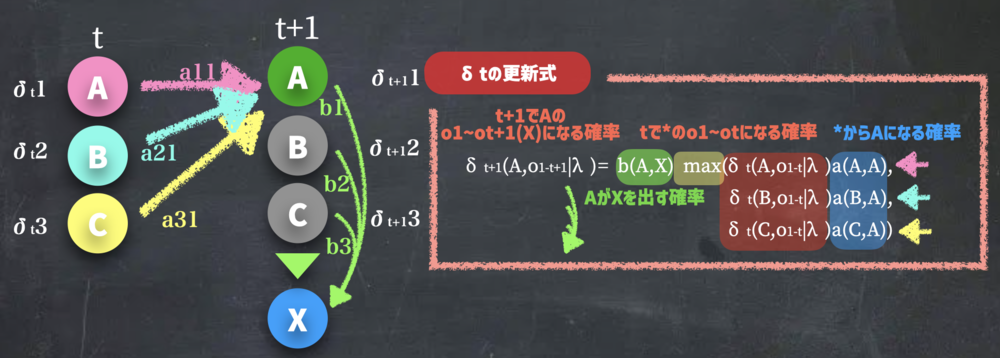 | δt+1の更新式.
仮にt+1でAになる場合の計算と図示. | ||||||||
$$\delta_{t+1}(A, O_{1-t+1}|\lambda) = b_A(X) max(\delta_t(A, O_{1-t}|\lambda) a_{AA} ,\delta_t(B, O_{1-t}|\lambda) a_{BA} ,\delta_t(C, O_{1-t}|\lambda) a_{CA} )$$
| δの更新式 | ||||||||
更新式は上式のようになっている.
これを最終的にt=Tまで行うと、上の例では、δT(A),δT(B),δT(C)が出揃うので、その中でも最も高い確率が選ぶことで、観測データから尤もらしいと思われる状態遷移列が得られる. | t=Tまで続ける | ||||||||
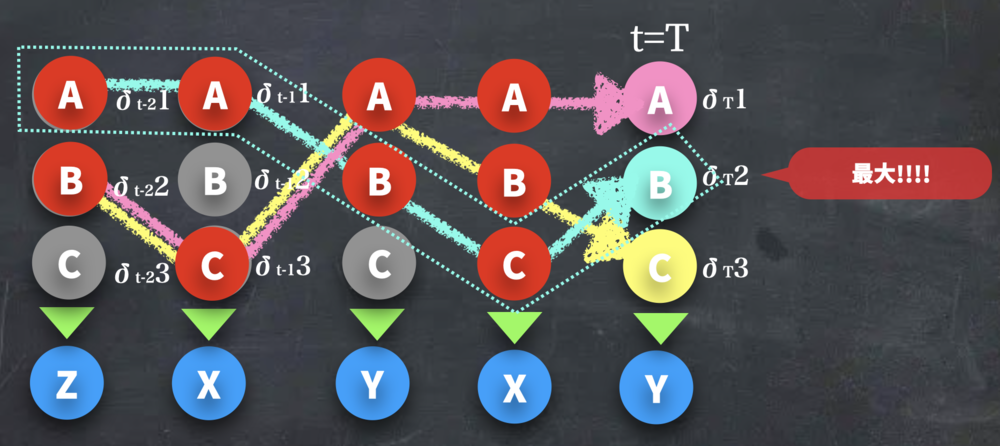 | 最後δT(B)が最も値が大きかった場合 | ||||||||
3.観測データと内部パラメータλから観測データの生成確率p(O|λ)を求める | |||||||||
なぜp(O|λ)を求めるかについて.
この意味は、あるパラメータの時に観測データ列Oができる確率を示します.
見方を変えると、この確率は現状得られたデータに最も適切なλであるかを示す評価関数とも捉えられそうです. つまり、この確率の値が大きくなるようなλは、観測データが出てきやすい値で尤もらしさがあります.
こういった関数を尤度と呼びます.
尤度関数に関しては下記の動画を参考にしてください. | なぜp(O|λ)を求めるか | ||||||||
一番わかりやすく解説された尤度関数の解説動画
【数分解説】尤度(尤度関数): あるデータが与えられる時そのデータが出やすいパラメータを求める評価値が欲しい【Likelihood Function】
| |||||||||
3.1.方法1 : 全てを足し合わせる | |||||||||
p(O|λ)はあるモデルのパラメータが与えられた時に、O="何か"の確率を求める関数です.
例えば、"ZXYY"という観測データが得られるのであれば、p(O="ZXYY"|λ)は、ZXYYが生成される確率を示します.
この確率を計算する最も簡単な方法は"内部状態の全てのケースを足し合わせる"です.
"内部状態の全パターンのそれぞれの確率"と、"各パターンの時にZXYYが生成される確率"が計算できれば、"ZXYYが生成される確率"はそれらを掛けて足し合わせるだけで求まります.
すなわち、
AAAA / AAAB / AAAC ..... ..... CCCA / CCCB / CCCC
の全部で3^4=81通りのケースで、それぞれの遷移確率を計算し、
さらにAAAAがZXYYを出力する確率などをそれぞれ求めて合算. | 全てを足し合わせる場合. | ||||||||
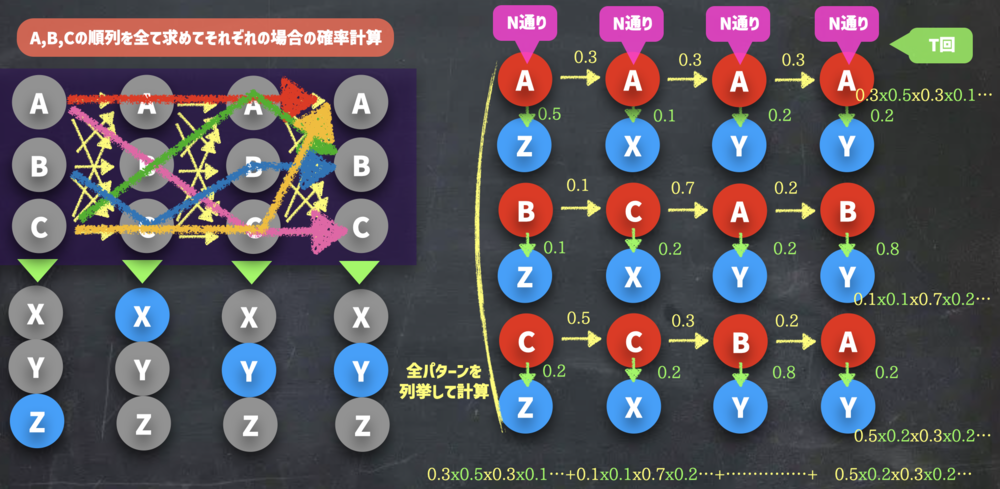 | 全パターンを計算して足し合わせ | ||||||||
しかしこの時、
$$O(2TN^T)$$
の計算量になります. | N通り(A,B,Cなら3)をT回の組み合わせのため、N^T.
さらにそれぞれの計算で、出力確率と遷移確率を掛け合わせるため、
TN^Tのオーダとなる | ||||||||
実はこの計算では、重複して同じ計算をしている箇所があるため、それを省いたアルゴリズムで効率的に求めることができます. | Forwardアルゴリズムへ | ||||||||
3.2.方法2 : Foward(Backward)アルゴリズムで動的計画法により算出 | |||||||||
Forwardアルゴリズムで\(p(O|λ)\)を計算していきます.
このアルゴリズムは、ビタビアルゴリズムと非常に似ていますのでそれを念頭に置いて下記を読んでください.
新しく\(\alpha_t(i)\)を定義します. これは、時刻tでiの状態で、0~tまでの間で観測データの\(O_0\)~\(O_t\)の出力を出す確率です.
式で表現するならば、
$$\alpha_t(i) = p(St=i, O_1O_2 \cdots Ot|\lambda)$$
となります. 時刻tでの状態iと時刻tまでの同時確率です.
この値を最後まで計算すると\(\alpha_T(i)\)が全ての状態に対して得られます.
$$\alpha_T(i) = p(S_T=i, O_1O_2 \cdots O_T |\lambda)$$
これが全ての状態\(S_T\)で得られているとすると、つまり
$$p(O|\lambda) = p(O_1O_2 \cdots O_T |\lambda) = \sum_{i=0}^I \alpha_T(i) = \sum_{i=0}^I p(S_T=i, O_1O_2 \cdots O_T |\lambda)$$
と全て足すことで、求めたかった値が得られることになります.(周辺化)
上記を最終的に得るために、このαを求めていきます. | αの導入 | ||||||||
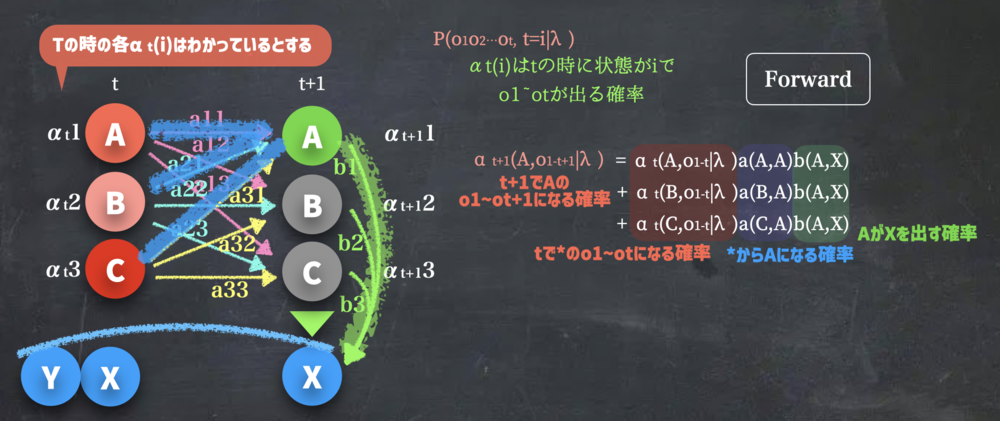 | αの更新.
αt+1(A,0|λ)のようにt+1においてAになるようなケースの計算 | ||||||||
$$\alpha_{t+1}(A, O_{1-t+1}|\lambda) = \alpha_{t}(A, O_{1-t}|\lambda)
a_{AA}b_A(X)\\ + \alpha_{t}(B, O_{1-t}|\lambda)
a_{BA}b_A(X) \\+ \alpha_{t}(C, O_{1-t}|\lambda)
a_{CA}b_A(X) $$ | αの更新式 | ||||||||
\(\alpha_{t+1}(i)\)を求めるにあたり、まず\(t\)の時のそれぞれの状態から遷移させる必要があります.tでi(A,B,C)だった時にj(A)に遷移する確率は、
$$\alpha_{t}(i) a_{ij}$$
と書けるはずです. そしてこの状態で、k(X)を出力をさせる確率は、
$$\alpha_{t}(i) a_{ij} b_{i}(k)$$
となる. 先ほどの\(\alpha \)の更新式はこれをtの時のiごとに全て足し合わせているに過ぎません.
$$\alpha_{t+1}(A, O_{1-t+1}|\lambda) = \sum_{i=A}^I \alpha_{t}(i) a_{ij} b_{i}(k)$$
を行なっていることになります.
これを\(t=0\)から\(t=T\)まで計算して、先ほどの\(\alpha_T(i) \)を得ます. | Forwardアルゴリズムの更新式概略. | ||||||||
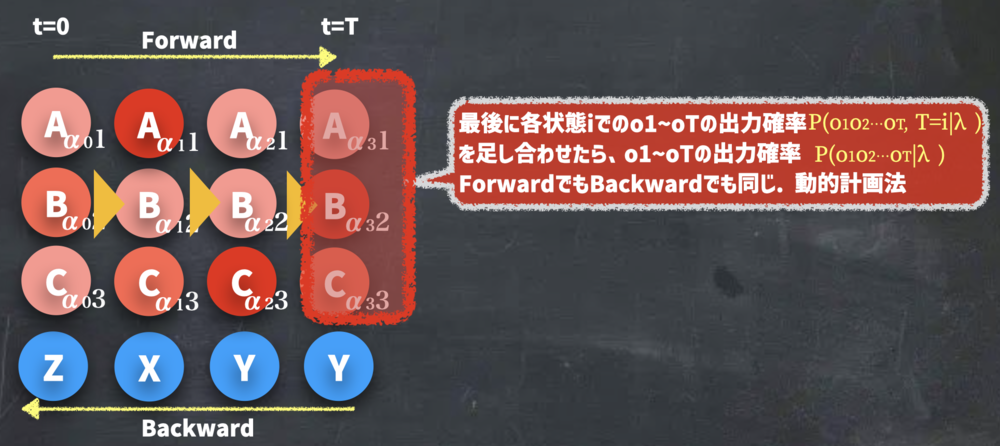 | ForwardをTまで順次計算した時の最後Tでの処理 | ||||||||
3.2.1.Backwardアルゴリズムで後向き確率を算出 | |||||||||
先ほどForwardアルゴリズムで求めたのは、前向き確率αでした.
今回はBackwardアルゴリズムで後向き確率βを求めます.
実は先ほどのαを求めたので、p(O|λ)はもう求めることができますが、BaumWelchの時に後向き確率も必要なので導出しておきます.
新しく\(\beta_t(i)\)をtの時にiと仮定した時の\(O_{t+1}\)~\(O_T\)が観測される確率とする.この時あくまでtの時のiは条件に過ぎないことに気を付けてください.
今度はt=Tからt=0に向かってβを計算していきます.
先ほどとは異なり、t=0の時のβの値を合計するとp(O|λ)が求まります. | Backwardアルゴリズム概要 | ||||||||
 | Backwardアルゴリズムのβtの更新式 | ||||||||
$$\beta_t(O_{t+1-T}|\lambda, A) = \beta_{t+1}(O_{t+2-T}|\lambda, A)a_{AA}b_A(X) \\ + \beta_{t+1}(O_{t+2-T}|\lambda, B)a_{AB}b_B(X) \\ +\beta_{t+1}(O_{t+2-T}|\lambda, C)a_{AC}b_C(X) $$ | βの更新式 | ||||||||
この処理を一部抽出すると
$$ \beta_{t+1}(O_{t+2-T}|\lambda, B)a_{AB}b_B(X) $$
を計算しています. これは一つ先の状態で\(\beta_{t+1}(O_{t+2-T}|\lambda, B)\) と求まった値に、\(a_{AB}b_B(X)\)をかけています.
$$ \beta_{t+1}(O_{t+2-T}|\lambda, B) = p(O=O_{t+2}O_{t+3} \cdots O_T| \lambda, B )$$
$$a_{AB} = p(B |A )$$
$$ b_B(X) = p(X|B )$$
であることから
$$ \beta_{t+1}(O_{t+2-T}|\lambda, B)a_{AB}b_B(X)\\
= p(O=O_{t+2}O_{t+3} \cdots O_T| \lambda, B )p(B |A ) p(X|B ) \\
= p(O=O_{t+2}O_{t+3} \cdots O_T| \lambda, B )p(X, B |A ) \\
= p(O=O_{t+2}O_{t+3} \cdots O_T, X, B| \lambda, A )\\
= p(O=XO_{t+2}O_{t+3} \cdots O_T, B| \lambda, A )\\
= p(O=O_{t+1}O_{t+2}O_{t+3} \cdots O_T, B| \lambda, A )
$$
となります.\(p(A,B) = p(A|B)p(B)\)によって式変形しています.
これを\(t+1\)の状態で周辺化すると、求めたい式が得られます.
$$\beta_t(i) = \sum_{i=A}^I \beta_{t+1}(O_{t+2-T}|\lambda, i)a_{Ai}b_i(X)\\
= \sum_{i=A}^I p(O=O_{t+1}O_{t+2}O_{t+3} \cdots O_T, i| \lambda, A ) $$
| 後向き確率の更新式の意図 | ||||||||
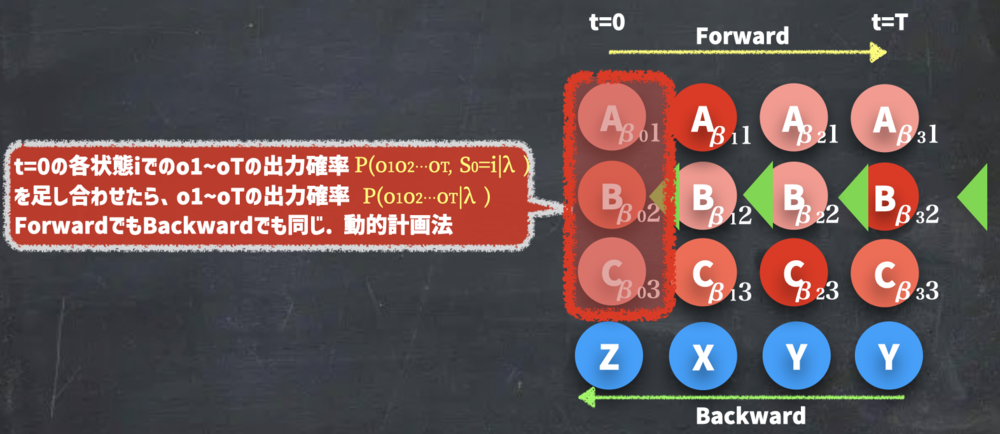 | Backwardで計算した時の最後に求まるt=0の計算 | ||||||||
4.観測データOから内部パラメータλを推定する | |||||||||
観測データOのみがある時にどのように内部パラメータを推定するかです.
先ほども話題に出たようにp(O|λ)を大きくするλは良いλに見えます.
しかし、観測できない状態のパラメータを解析的に求めるのは難しいことは若っいるため、逐次的な計算で次第に良いパラメータに変えていく方法がとられます.
その代表的な方法にEMアルゴリズムがあります.
今回の更新処理もEMアルゴリズムのEステップ、Mステップに沿って処理をすることになります. | 内部パラメータ推定の概要 | ||||||||
4.1.Baum Welch アルゴリズム | |||||||||
まずBaum Welchアルゴリズムで内部パラメータを求める概要を紹介します.
1. a, bなどを初期値をセット
2. a,bを使ってα,βを計算
3. その値をもとに"tでi,t+1でjとなる確率ξ"を計算
4. さらに"ξ"をt+1の状態で周辺化して、"tでiとなる確率γ"を計算
5. γとξを使って、a,bの値を更新.
6. 2から繰り返し
と計算し、p(O|λ)が更新されなくなれば、パラメータの更新は終了です.
どういうことか、もう少し詳しく見てみましょう. | BaumWelchアルゴリズムの処理概要 | ||||||||
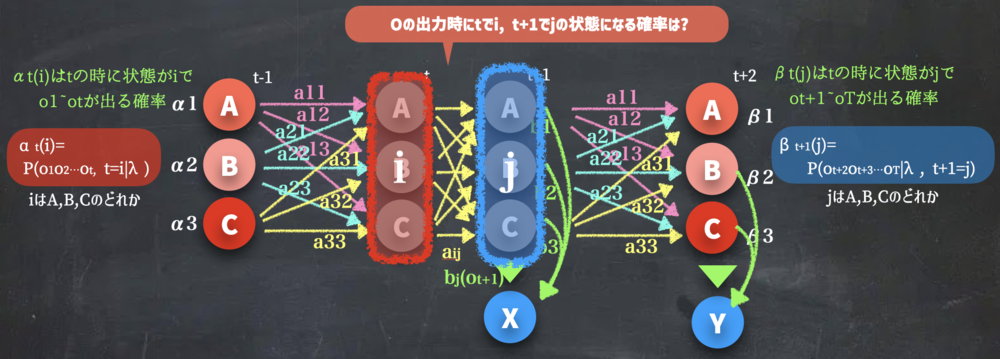 | Baum Welchアルゴリズムでまずはξを求める準備.
αt(i)とβt+1(j)を使う | ||||||||
BaumWelchでは、まずtでiかつ\(t+1\) でjかつ\(t+1\) で\( k\)となるような確率ξを計算します.
これは、つまり
$$\xi = \alpha_{t}(i)a_{ij}b_{j}(k)\beta_{t+1}(j)$$
これは上記の画像のように左側まではαで確率が求まり、右側はβで確率が求まるので、あとは繋ぎ部分を計算することで\(\xi\)を計算できます. | ξの計算まとめ | ||||||||
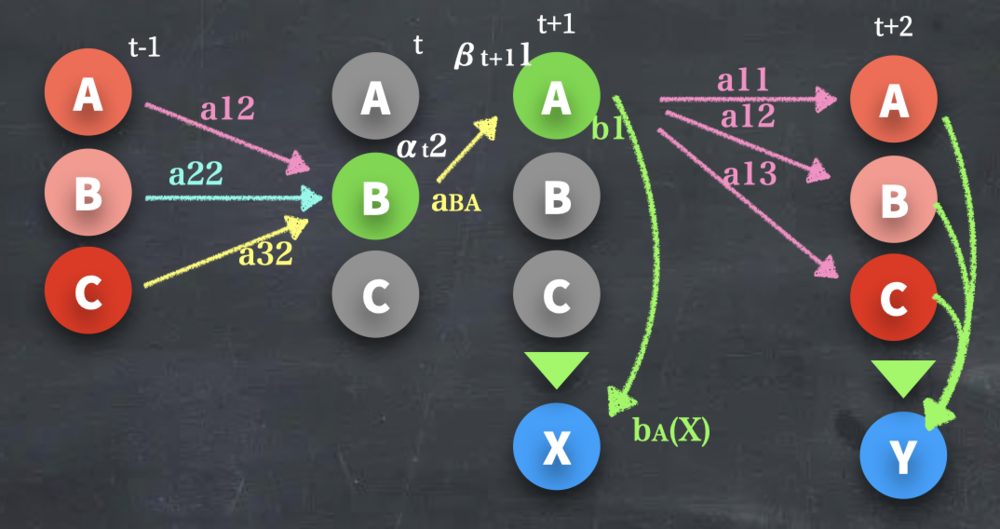 | 上記をi=B, j=Aだった場合はこのような確率を求めることになります.
αt(B) aBA bA(X) βt+1(A) | ||||||||
そしてこの\(\xi\)の和をt+1のjで取ると、"tでiになる確率γ"が計算できます.
$$\gamma_t(i) = \sum_{j=A}^{J} \xi_t(i,j ) =\sum_{j=A}^{J} p(S_t=i, S_{t+1}=j|\lambda, O_{1-T} )=p(S_t=i|\lambda, O_{1-T} )$$
この\(\gamma_t(i)\)はつまり、今までの図における各丸の確率が求まったことになります.
時刻tで状態がiになっている確率が求まっているので、これを\(O\)~\(T\)で足し合わせると、"一連の観測データを得る間に状態iに\(O\)~\(T\)で何回なるかの期待値"になります. | γの計算 | ||||||||
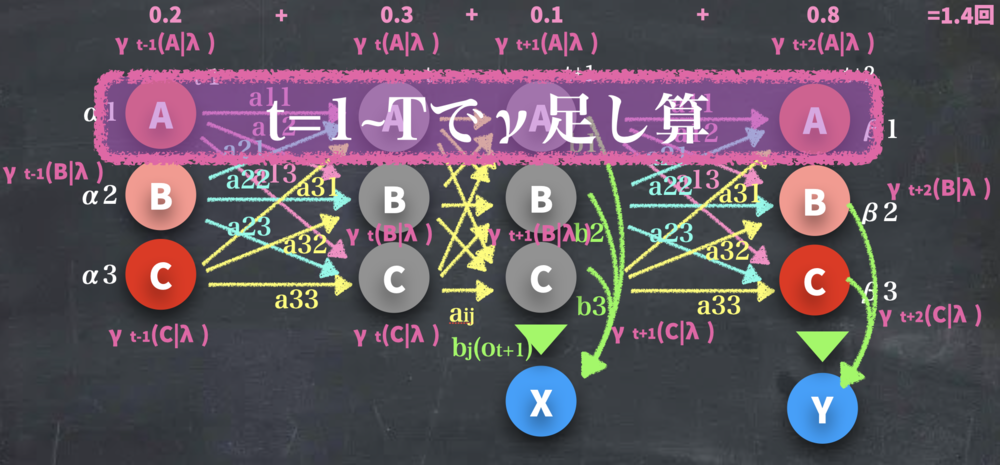 | γの足し合わせ処理.
γt-1(A)- γt+2(A)=1.4となっており、この期間でのAの出現期待値は1.4回とわかる | ||||||||
同様に\(\xi\)をtで足した場合も同様に"一連の観測データを得る間に状態iから状態jに何回変わったかの期待値"が得られます.
$$\sum_{t=0}^{T} \xi_t(i,j) $$
これを先ほどの計算と合わせると、
$$a_{ij} = \frac{\sum_{t=0}^{T} \xi_t(i,j)}{\sum_{t=0}^{T} \gamma_t(i)}=\frac{t=0からTまでに何回i→jになったか}{t=0からTまでに何回iになったか}$$
となることがわかります.AからA,B,Cにそれぞれ遷移した回数が分かれば、比率が求まるので遷移確率\(a_{ij}\)となることがわかります. | aijの更新 | ||||||||
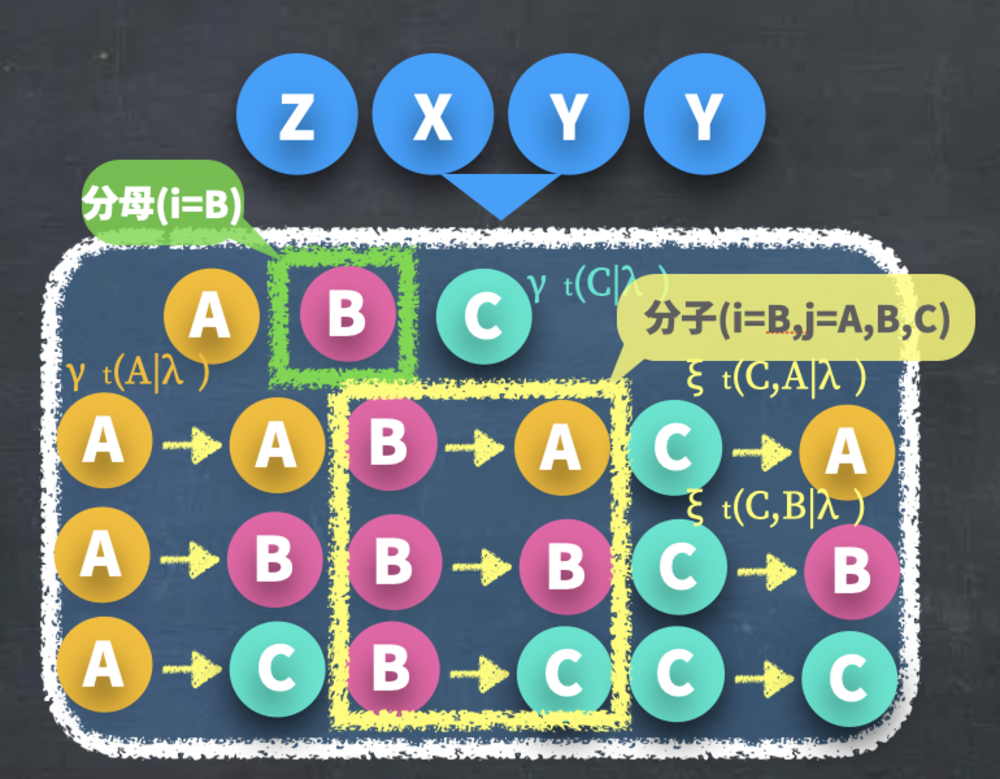 | ZXYYが観測された時のそれぞれの遷移と状態 | ||||||||
同様な考えで\(b_i(k)\)も求まります.
$$b_i(k) = \frac{\sum_{t=0 and Ot=k }^T \gamma_t(i)}{\sum_{t=0}^T \gamma_t(i) } = \frac{t=0からTまでに何回iがkを出力したか}{t=0からTまでに何回iになったか}$$
分子では全てのtで足すのではなく、出力がkになったγだけ足し込みます.
これによって、何回中何回kが出力されたかがわかり、すなわち出力確率\(b\)
を求めたことになります. 分母も分子も期待値になっているのでご注意ください. | bの更新 | ||||||||
EMアルゴリズムでいうEStepは、γとξを計算しているフェーズで
EMアルゴリズムでいうMStepは、aとbを更新しているフェーズです.
(MStepの期待値の分数の計算は、モデルの式の極値の計算式として導かれたものです. )
このようにa,bを更新することで必ずp(O|λ)が大きくなっていくことが保証されています. これでBaumWelchアルゴリズムは適切なλを推測することができます.
| EMアルゴリズムとの対応 |
この章を学んで新たに学べる
Comments


