-
 @ThothChildren
@ThothChildren
- 2018.5.23
- PV 1525
点群データから法線算出をしたい
ー 概要 ー
センサ等から得られる点群データを入力として法線を算出したいときに使用する技術についてまとめます.

この章を学ぶ前に必要な知識
条件
- 3次元点群データを入力
- どこまでを参考にして法線を計算するかの近傍の距離を決める
効果
- 点群の法線を得る
ポイント
- 手法によってノイズに弱かったりするので注意
解 説
点群処理やCGにおいては法線計算が欠かせないです.CGにおいては既にモデルの表面の平面等があるので法線はその平面等を元に算出できますが、
点群処理の場合はどの点とどの点がどちらに平面を張っているか分からない状態で法線を推定することになります.
法線推定で見られる手法には以下のようなものがあります.
<手法>
・まず表面を作成してからその表面の法線を求める
ノイズに弱い
・特定の領域の点群に対して平面をフィッティングし、その法線
最小二乗法を用いて局所的な点群の集まりに対してフィッテングします.ノイズに若干強い
・点群データで点が伸びている平面方向を求めてその法線
PCL(PointCloudLibrary)で用いられている方法.PCAによって平面を決定します.
上記の点が主な手法の違いになりますが、細かな工夫は様々あります.
例えば、
・法線が同じ表面なら同じ方向を向くようにする.
・立方体の淵で中途半端な方向を向いてしまうのをそろえる.
といったことが行われます.
| 点群データから法線算出をしたいの導入 |
1.表面を作成して法線を求める | |
表面を作成してCGの表面のようにしてから法線を求める手法になります.
こちらを行った場合は、Coconeといった有名な表面復元(Surface Reconstruction)をまず行います.
その後求められたメッシュからその法線を求めます. | 表面を作成して法線を求める |
Surface Reconstructionは点群データから表面を作る技術を指します.
それらの技術はCoconeに限らず様々な手法があります.
有名なCoconeやCrustはVoronoiベースの手法になります.VoronoiではないものにはPoissonによるimplicit surfaceに基づくもの等があげられます.
| 表面復元(Surface Reconstructionについて) |
 | 点群からのメッシュ生成 |
メッシュが作成され各点とその三角形の関係が得られれば後は簡単です.
\(\vec{x_1}\)と\(\vec{x_2}\)がその三角形の成す2辺だとすれば、その法線は二つのベクトルの外積で求まります.
$$\vec{ x_1 } \times \vec{ x_2 }$$ | メッシュから三角形を取り出し、その法線を算出 |
2.局所点群に対して平面をフィッティングし法線生成 | |
こちらもイメージはしやすいと思います.
平面を局所的に切り抜いた点群に対してフィッテングする方法です.最小二乗法などの有名な方法で平面をフィッティングして、その平面の向きを法線とすれば良さそうです.
こちらは上記の「表面を作成して法線を求める」よりは当然ノイズには強くなりますが、フィッティングする手法によってはノイズに弱くなります.最小二乗法は弱い方になると思います. | 局所点群に対して平面をフィッティング |
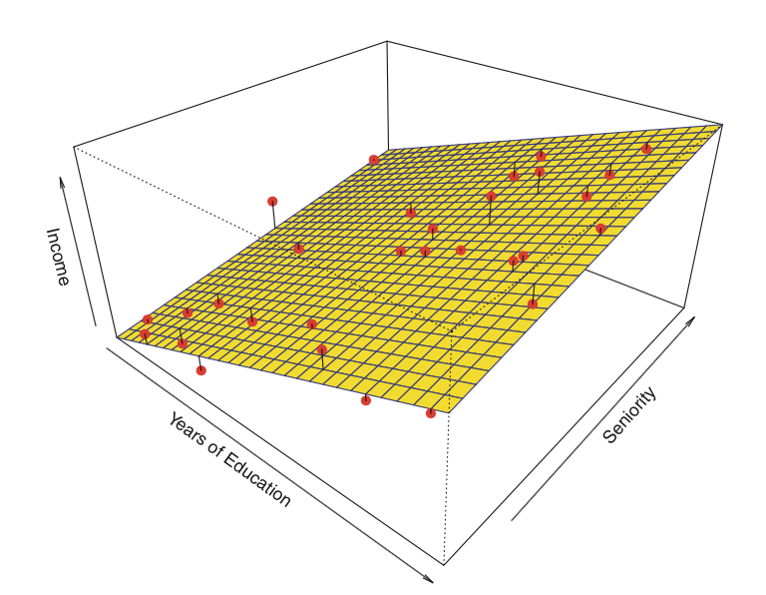 | 平面フィッティングのイメージ |
右は平面に限らず一般的な関数近似手法についてお手軽なものがまとまっています. | 関数既知で多数データの関数近似したい |
3.点群が伸びている方向を平面として法線生成 | |
こちらはPCL(Point Cloud Library)でも採用されている法線推定の手法になります.
この手法では表面の生成や平面のフィッティングを行うことなく、点群データのみを使用して、法線を求めます.
まず、点群に対してPCAを行い法線が垂直になっている面の方向(2軸)を求めます.PCAを用いると最もデータ伸びていて分散が広い方向を見つけることができるため、接平面を見つけたような状態になります.
その二つのベクトルが分かってしまえば後は「1.」の法線ベクトルを求める処理と同様の流れになります.
| 点群の伸びている方向を平面として法線生成 |
 | PCLにて求められた法線 |
この章を学んで新たに学べる
Comments
Reasons
知識: 関数既知で多数データの関数近似したい
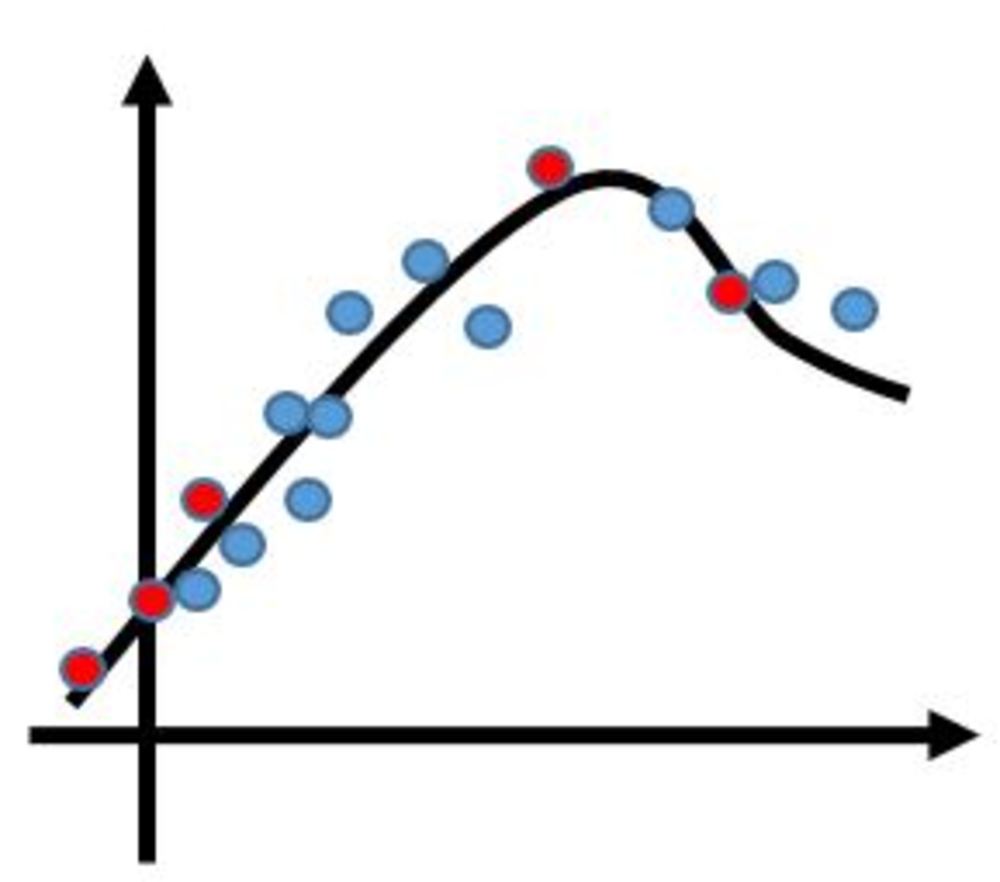
データの当てはまりがよさそうな関数が既知で多数のデータが与えられるときに、それらのデータを用いて関数近似をする方法についてまとめます.比較的単純で代表的な技術のみにとどめます.


