グラムシュミットの正規直交化法

グラムシュミットの正規直交化法は与えられたベクトル\(a_0 \cdots a_n \)を用いてお互いに直交した正規化ベクトル\(e_0 \cdots e_n \)を求める手法です. QR分解等でグラムシュミットの正規直交化法は利用されます. 手順概要 1. \(a_0\)を\(u_0\)とします. 2. i回目の処理: \(a_i\)から今まで算出した\(u_0 \cdots u_{i-1} \)と平行なベクトルの成分を引いて、それらのベクトル全てに直交するようにします.それを新しい\(u_i\)とします. 3. 2.を最後のnまで繰り返します.

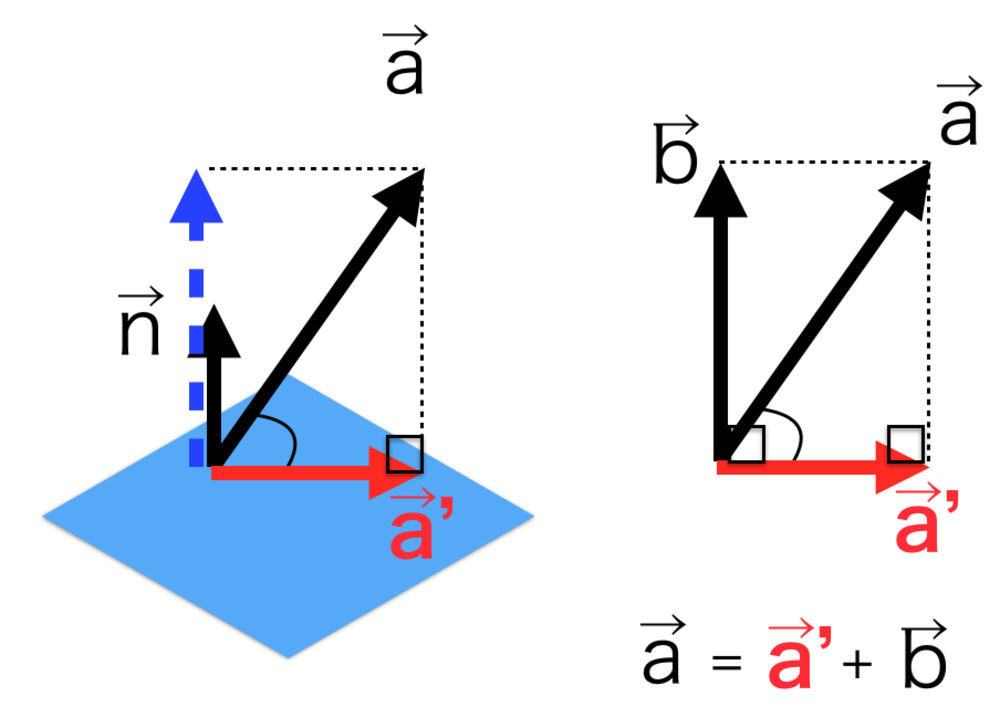
上記の2番目の処理は右の平面にベクトルを写像する処理と非常に似ているため、理解する上で一度目を通しておくと把握しやすいかと思います. 平面にベクトルを射影するときには、与えられたベクトルから平面の法線方向の成分を引いてました. 今回はそれらを今まで求めた全てのベクトルに対して行うのみです.それによってベクトルが平面の法線ベクトルに直交したように、全ての他のベクトルに直交することになります.

数式を使って上記の手順概要を補っておきます.ここでは3次元ベクトルの場合の手順を書いておきます. 1. \(u_0 = a_0\) 2. \(u_1 = a_1 - \frac{u_0 \cdot a_1}{u_0 \cdot u_0}u_0\) 2.の処理で\(a_1\)から\(u_0\)に平行な成分を引いています.\(u_0\)の成分を全く持たない\(u_1\)は\(u_0\)に直交します. 3. \(u_2 = a_2 - \frac{u_0 \cdot a_2}{u_0 \cdot u_0}u_0- \frac{u_1 \cdot a_2}{u_1 \cdot u_1}u_1\) 上記のように導くことで\(u_0, u_1, u_2\)の3つのベクトルが求まります. それぞれ\(u_0\)は\(a_0\)のみの線形結合、\(u_1\)は\(a_0\)と\(a_1\)の線形結合、 \(u_1\)は\(a_0\)と\(a_1\)と\(a_2\)の線形結合で表現されています. 直交の確認 \(u_1\)と\(u_0\)の直交を確認します.直交は内積が0になればよいです. $$u_1\cdot u_0 = (a_1 - \frac{u_0 \cdot a_1}{u_0 \cdot u_0}u_0)\cdot u_0 = a_1\cdot u_0 - \frac{u_0 \cdot a_1}{u_0 \cdot u_0}(u_0\cdot u_0)=0 $$ 簡単に確認することができました. 上記二つのベクトルは直交しています. もっと高次元 もっと高次元の場合は上記の2.や3.と同様の処理を繰り返すだけです.

正規直交化のうち直交化について上では求めました. 正規化においては、以下のように自身の大きさで割ることで大きさが1になるようにします. $$e_i = \frac{u_i}{|u_i|}$$

\(a_0 = (1,2,1), a_1 = (2,0,1), a_2=(0,1,2)\)の場合. $$u_0 = (1,2,1)$$ $$u_1 = (2,0,1) - \frac{( 1,2,1 )\cdot (2,0,1)}{|( 1,2,1 )|^2}(1,2,1) = (\frac{3}{2}, -1, \frac{1}{2})$$ $$u_2 = (0,1,2) - \frac{( 1,2,1 )\cdot (0,1,2)}{|( 1,2,1 )|^2}(1,2,1)- \frac{(\frac{3}{2}, -1, \frac{1}{2})\cdot (0,1,2)}{|(\frac{3}{2}, -1, \frac{1}{2})|^2}(\frac{3}{2}, -1, \frac{1}{2})$$ $$ = (-\frac{2}{3}, -\frac{1}{3}, \frac{2}{3})$$