運動学

運動学はロボットの関節角とロボットの手先位置の幾何的関係に関するもので、一方からもう片方を求める順運動学や逆運動学があります.

2018.7.17

105

Views
0

Watch
5

Knows

ロボットの手先の位置、姿勢からロボットの関節角度を求める逆運動学に関してまとめたページです.一般に複数の解を持ち、また簡単な設定では解析的に解くことが可能ですが多くのケースにおいては解析的に解くのが困難なため探索的に解を求めます.

運動学周辺知識

運動学に関連する分野周辺の単語、知識に関してまとめたページになります.逆運動学や順運動学で頻出する単語をまとめます.

運動学の新規投稿

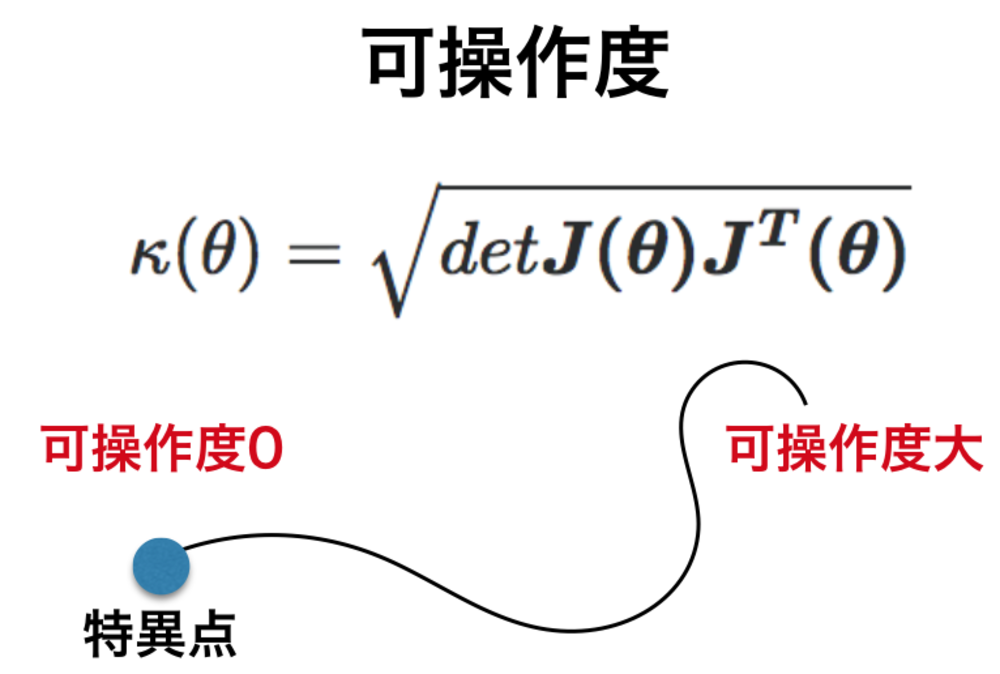
可操作度は特異点を避けたいときに指標となる特異点との距離に当たるような数値を求められる.特異点において可操作度の値は0となる.ヤコビ行列Jを用いて求めることが可能.

SR-Inverse(Singularity-Robust Inverse)は特異点に近くなるにつれてヤコビ行列がフルランクではなくなりロボットの動きが大きくなってしまうのを防ぐために擬似逆行列を別行列に置き換えた逆運動学.特異点まわりを避け大きな運動をしないようにすることが可能.

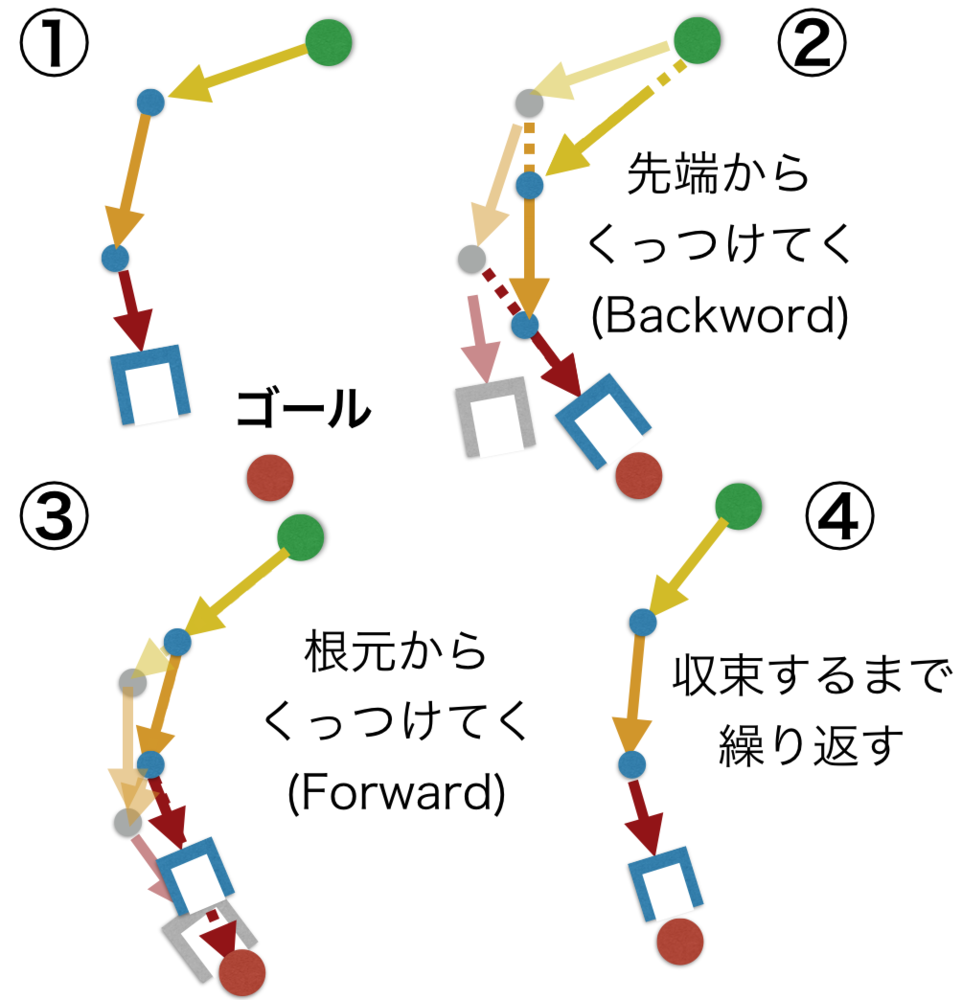
FABRIKによる逆運動学

FABRIK IK(Forward And Backward Reaching inverse kinematics)は、根元と先端を交互に基準として繰り返しながら関節角度を調整していくことで、逆運動学の解を得る.アルゴリズムはシンプルで、実装も容易い.

CCDによる逆運動学

Cyclic-Coordinate-Descent法(CCD法)を用いた逆運動学についてまとめます.CCDでは単純な計算を繰り返していくことで手先位置に合う関節角度を求めることができます.手先位置の姿勢は指定できずあくまで位置のみ合わせにいきますが、軽量なアルゴリズムです.CCDでも局所最適解にはまるケースがあります.

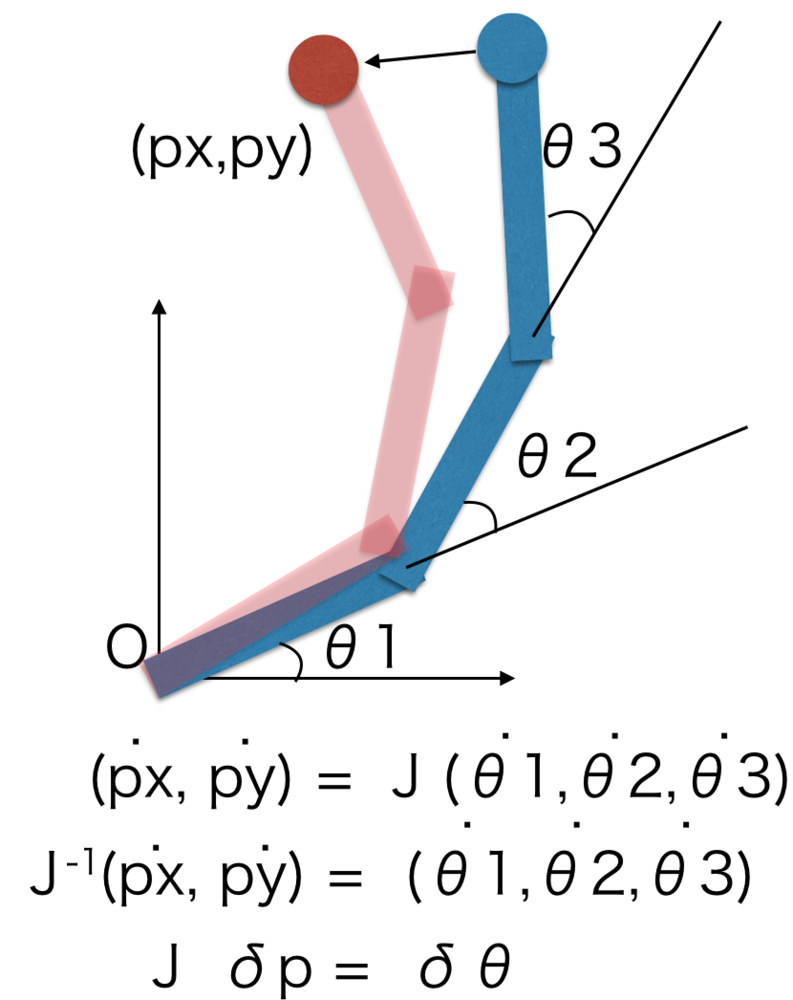
ヤコビ行列による逆運動学

関節角度と手先位置のp=f(θ)の関係からδθ=J^-1()δp(Jはヤコビ行列)を導きこの勾配を利用して近似的に関節角を探索する方法についてまとめます.一般的に逆運動学は解析的に解けないため、このような繰り返し計算による解の導出を行います.ヤコビ行列による逆運動学はその中でも最も有名な手法です.

運動学人気知識・質問

ヤコビ行列による逆運動学

関節角度と手先位置のp=f(θ)の関係からδθ=J^-1()δp(Jはヤコビ行列)を導きこの勾配を利用して近似的に関節角を探索する方法についてまとめます.一般的に逆運動学は解析的に解けないため、このような繰り返し計算による解の導出を行います.ヤコビ行列による逆運動学はその中でも最も有名な手法です.

FABRIKによる逆運動学

FABRIK IK(Forward And Backward Reaching inverse kinematics)は、根元と先端を交互に基準として繰り返しながら関節角度を調整していくことで、逆運動学の解を得る.アルゴリズムはシンプルで、実装も容易い.

可操作度は特異点を避けたいときに指標となる特異点との距離に当たるような数値を求められる.特異点において可操作度の値は0となる.ヤコビ行列Jを用いて求めることが可能.

SR-Inverse(Singularity-Robust Inverse)は特異点に近くなるにつれてヤコビ行列がフルランクではなくなりロボットの動きが大きくなってしまうのを防ぐために擬似逆行列を別行列に置き換えた逆運動学.特異点まわりを避け大きな運動をしないようにすることが可能.

CCDによる逆運動学

Cyclic-Coordinate-Descent法(CCD法)を用いた逆運動学についてまとめます.CCDでは単純な計算を繰り返していくことで手先位置に合う関節角度を求めることができます.手先位置の姿勢は指定できずあくまで位置のみ合わせにいきますが、軽量なアルゴリズムです.CCDでも局所最適解にはまるケースがあります.