©2024 Thoth Children All rights reserved.

グラフの探索

データをグラフの形状で表現できているときにそのグラフの中で目的に沿った経路やデータを見つけ出す探索アルゴリズムについてまとめています. 幅優先探索や深さ優先探索などもこれらのグラフ探索の種類で、ダイクストラ方やベルマンフォートなどの最小コスト経路の探索もこの中で紹介します.
2018.7.22
  • 89
    Views
  • 0
    Watch
  • 8
    Knows

グラフの探索の新規投稿

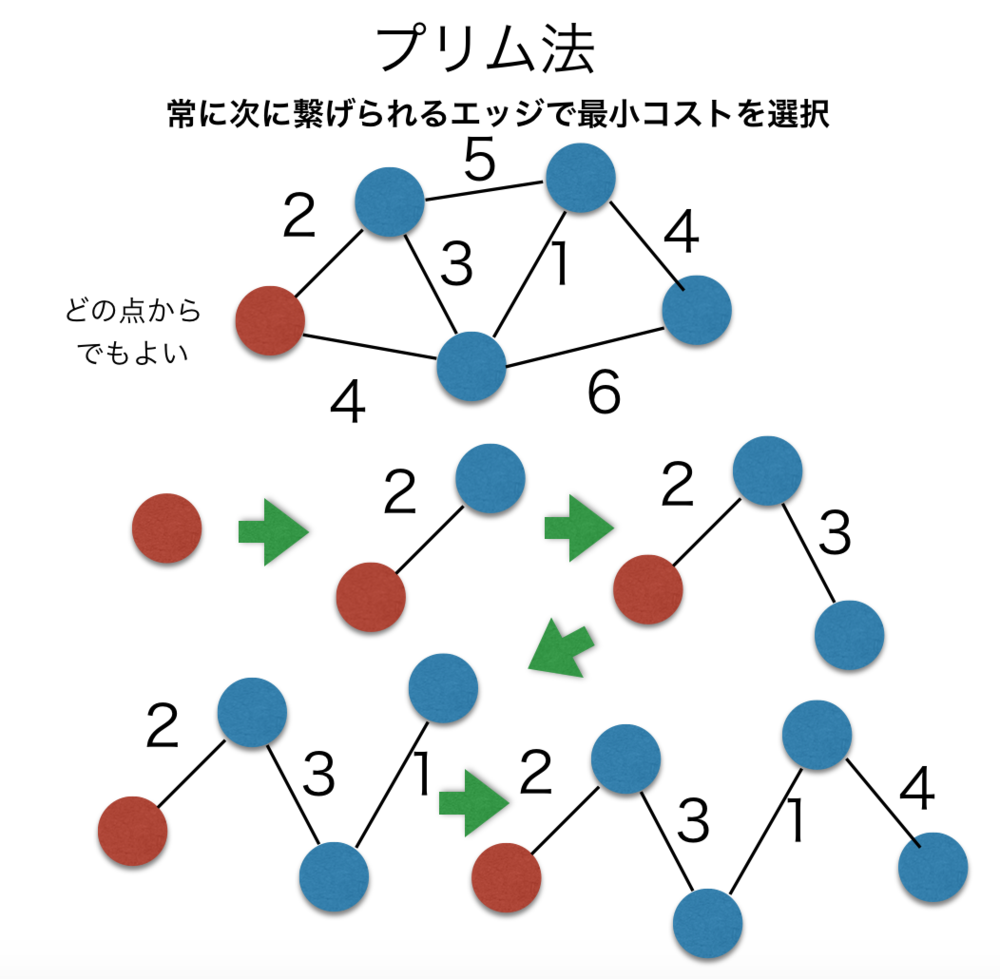
プリム法
プリム法は、最小全域木を求める貪欲法ベースで時間計算量がO(E+V log V)となる探索アルゴリズム.時間計算量は実装方法に依存する.特定の点から始めて常に繋がりうるエッジのうち最小のコストのエッジを選択することを繰り返す.
PV 216
Fav 0
2018.11.07
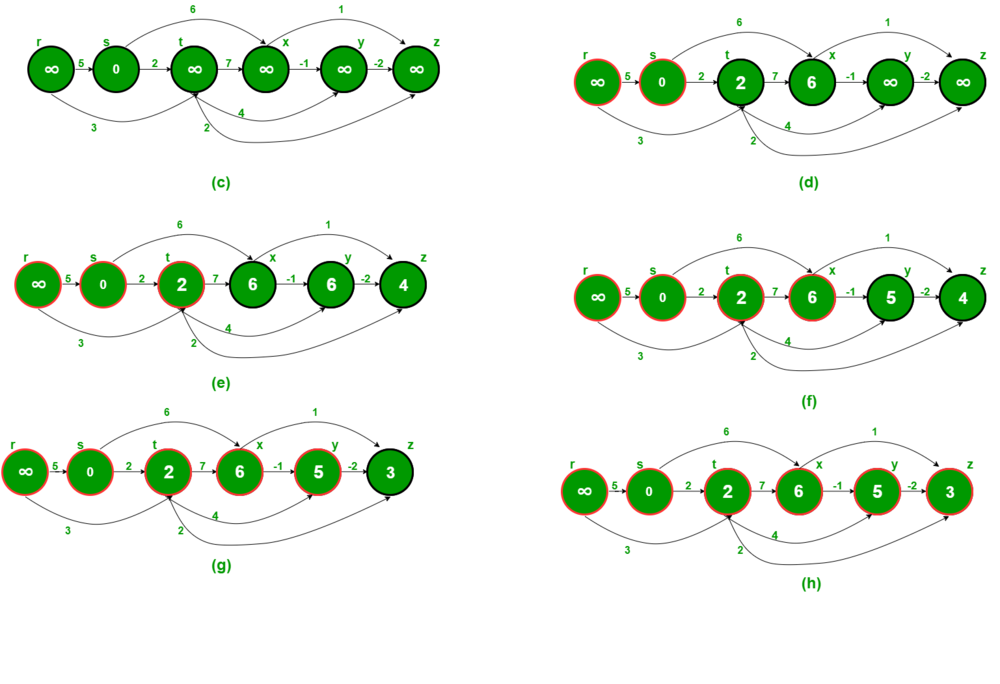
トポロジカルソートのDAG経路探索
有向非循環グラフ(DAG)の最短経路探索を線形時間で探索を行う手法として、トポロジカルソートによるものが挙げられます.一度しかノードもエッジも参照しないため、ソート自体もその後の最短経路探索も線形時間で探索が完了します.
PV 215
Fav 0
2018.10.21
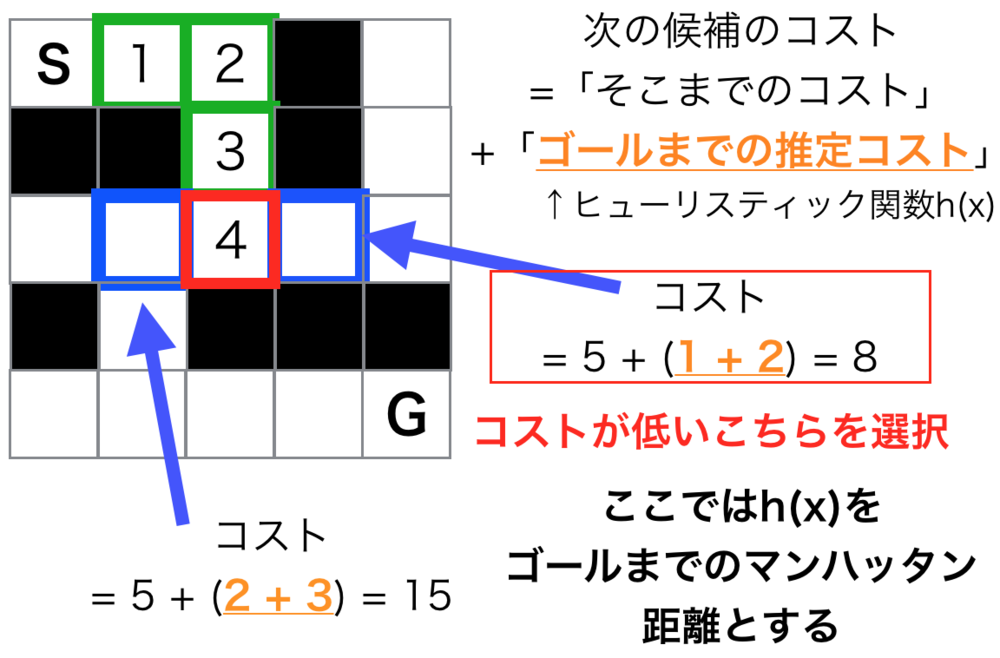
A*探索アルゴリズム
A*探索アルゴリズムは候補のノードのうち「それまでのコスト」+「ゴールまでの推定コスト」が最小になると思われるノードを繰り返し選択していき効率的に最短経路を探索するアルゴリズム.ダイクストラの一般化であり、「ゴールまでの推定コスト」を0にしているのがダイクストラ法.「ゴールまでの推定コスト」は自身で決める必要があり、その質に探索の効率が大きく左右される.
PV 385
Fav 0
2018.08.08
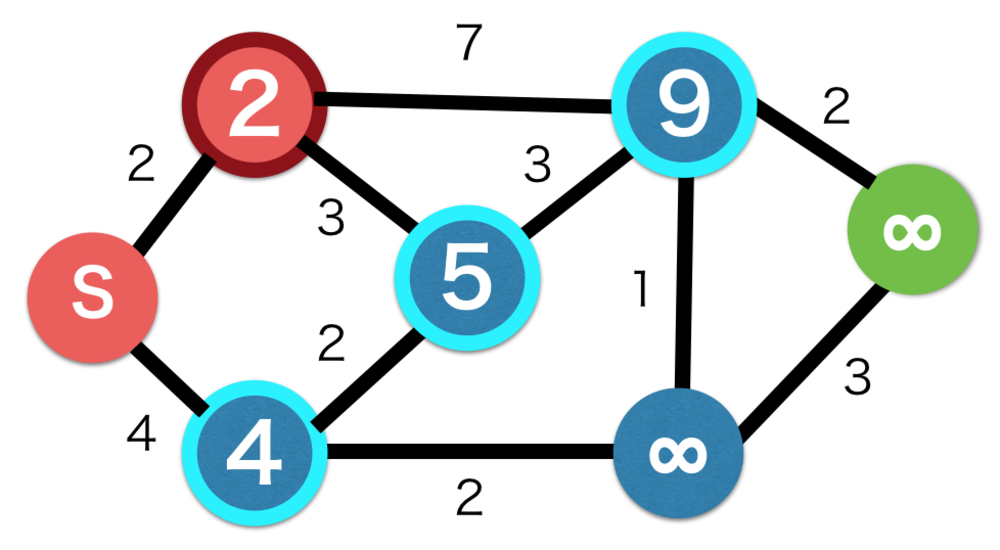
ダイクストラ法
ダイクストラ法は、負のコストがない回路において、ルートを選択を工夫して最短経路を見つけ出していくことで、ベルマンフォード法より効率的に探索することのできるアルゴリズム.普通の実装では計算量はO(n^2)だが、適当なヒープを用いることでO(E+nlog(n))になる.
PV 294
Fav 0
2018.08.08
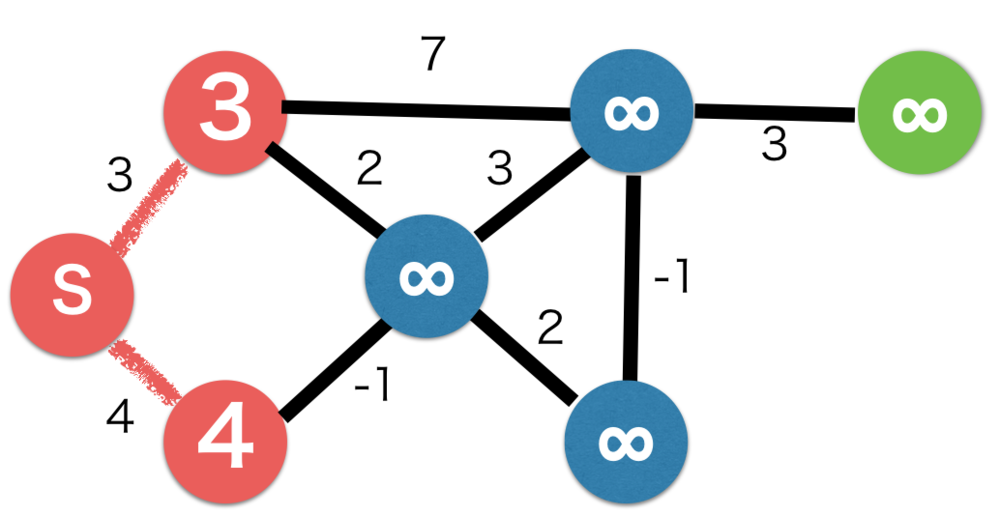
ベルマンフォード法
ベルマンフォード法は、コストがついた辺をもつグラフにおいてある始点からある終点までの最短コストの経路を探索するアルゴリズムです.ベルマンフォードはダイクストラと異なり負の値も扱うことができます.もし一周したコストが負になる箇所があるとそこをぐるぐる回り続けることによっていくらでもコストを避けられるため、そのようなグラフでは解を持ちません.
PV 540
Fav 0
2018.07.24
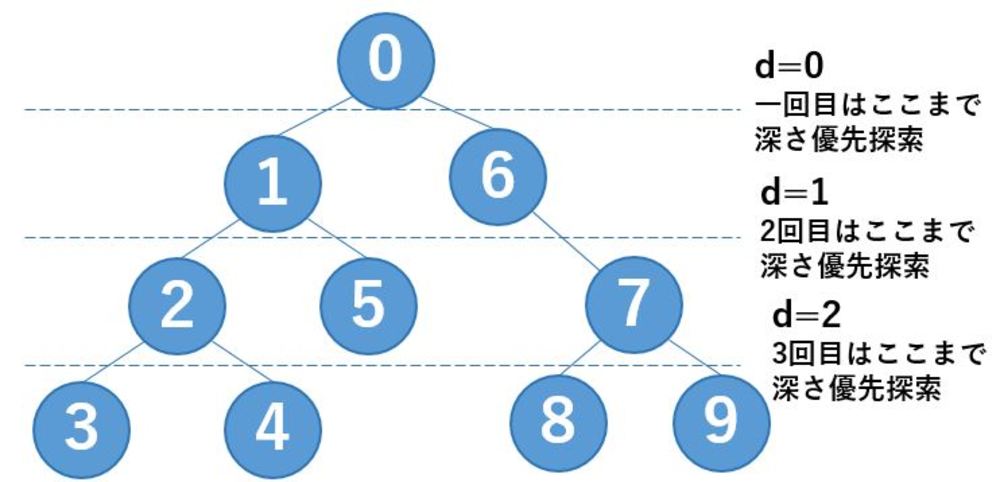
反復深化探索
反復深化探索(反復深化深さ優先探索, ID, Iterative deepening depth-first search)は深さを制限した深さ優先探索を最大深さ0から次第に大きくしながら目的のデータが見つかるまで繰り返す探索.深さ優先のメモリの効率性と幅優先探索の完全性、最適性を備え持っているため、深さ優先探索や幅優先探索よりも理論上優れていることが多い.
PV 1079
Fav 0
2018.07.22
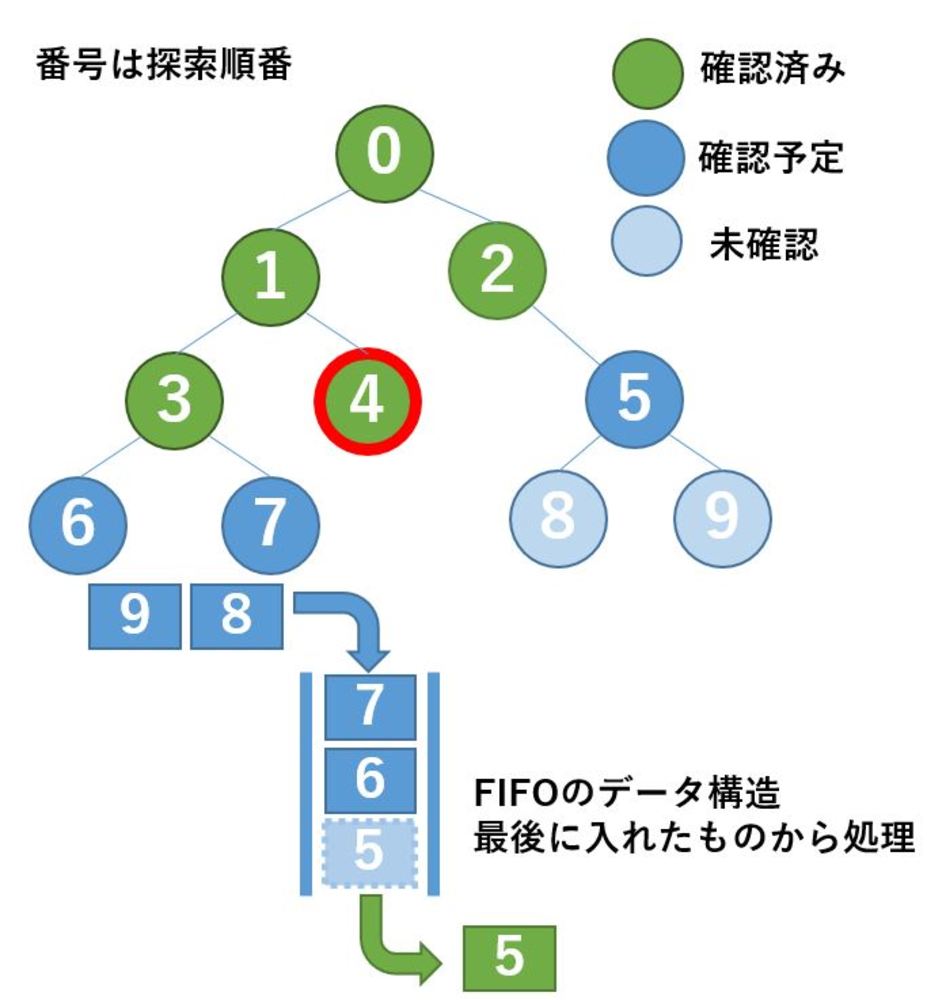
幅優先探索
幅優先探索はグラフデータの中でスタートのデータから浅いデータから探索し、見つからなければ更に深いところで次の候補を探していく探索.今まで見てきたデータを保持するため空間計算量が大きく、頂点数VでO(V)、または深さdと平均分岐数bを用いてO(b^d)と記述できます
PV 140
Fav 0
2018.07.22
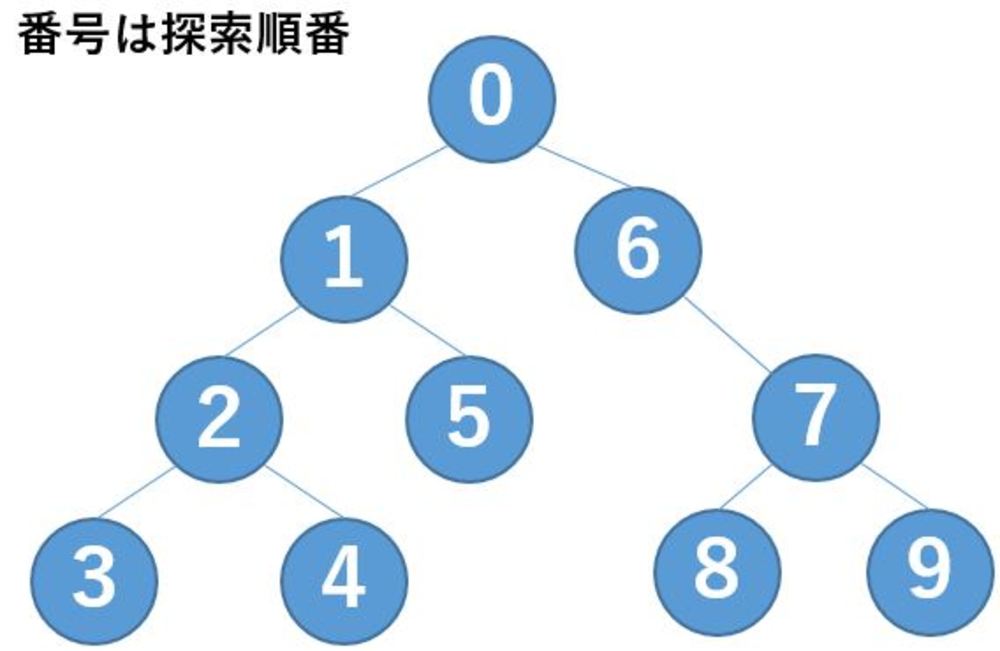
深さ優先探索
深さ優先探索はグラフデータの中でスタートのデータからとりあえずグラフの分岐がなくなるまで探索し、なくなったら少し戻って次の候補を探していく探索.データが深いところにありうる場合には幅優先探索でなくこちらを使用します.際限なく深くなりそうなときは最大深さを決めて途中で打ち切る場合もあります.通常幅優先探索より空間計算量ははるかに小さくなる.
PV 280
Fav 0
2018.07.22

グラフの探索人気知識・質問

反復深化探索
反復深化探索(反復深化深さ優先探索, ID, Iterative deepening depth-first search)は深さを制限した深さ優先探索を最大深さ0から次第に大きくしながら目的のデータが見つかるまで繰り返す探索.深さ優先のメモリの効率性と幅優先探索の完全性、最適性を備え持っているため、深さ優先探索や幅優先探索よりも理論上優れていることが多い.
PV 1079
Fav 0
2018.07.22
ベルマンフォード法
ベルマンフォード法は、コストがついた辺をもつグラフにおいてある始点からある終点までの最短コストの経路を探索するアルゴリズムです.ベルマンフォードはダイクストラと異なり負の値も扱うことができます.もし一周したコストが負になる箇所があるとそこをぐるぐる回り続けることによっていくらでもコストを避けられるため、そのようなグラフでは解を持ちません.
PV 540
Fav 0
2018.07.24
A*探索アルゴリズム
A*探索アルゴリズムは候補のノードのうち「それまでのコスト」+「ゴールまでの推定コスト」が最小になると思われるノードを繰り返し選択していき効率的に最短経路を探索するアルゴリズム.ダイクストラの一般化であり、「ゴールまでの推定コスト」を0にしているのがダイクストラ法.「ゴールまでの推定コスト」は自身で決める必要があり、その質に探索の効率が大きく左右される.
PV 385
Fav 0
2018.08.08
ダイクストラ法
ダイクストラ法は、負のコストがない回路において、ルートを選択を工夫して最短経路を見つけ出していくことで、ベルマンフォード法より効率的に探索することのできるアルゴリズム.普通の実装では計算量はO(n^2)だが、適当なヒープを用いることでO(E+nlog(n))になる.
PV 294
Fav 0
2018.08.08
深さ優先探索
深さ優先探索はグラフデータの中でスタートのデータからとりあえずグラフの分岐がなくなるまで探索し、なくなったら少し戻って次の候補を探していく探索.データが深いところにありうる場合には幅優先探索でなくこちらを使用します.際限なく深くなりそうなときは最大深さを決めて途中で打ち切る場合もあります.通常幅優先探索より空間計算量ははるかに小さくなる.
PV 280
Fav 0
2018.07.22
プリム法
プリム法は、最小全域木を求める貪欲法ベースで時間計算量がO(E+V log V)となる探索アルゴリズム.時間計算量は実装方法に依存する.特定の点から始めて常に繋がりうるエッジのうち最小のコストのエッジを選択することを繰り返す.
PV 216
Fav 0
2018.11.07
トポロジカルソートのDAG経路探索
有向非循環グラフ(DAG)の最短経路探索を線形時間で探索を行う手法として、トポロジカルソートによるものが挙げられます.一度しかノードもエッジも参照しないため、ソート自体もその後の最短経路探索も線形時間で探索が完了します.
PV 215
Fav 0
2018.10.21
幅優先探索
幅優先探索はグラフデータの中でスタートのデータから浅いデータから探索し、見つからなければ更に深いところで次の候補を探していく探索.今まで見てきたデータを保持するため空間計算量が大きく、頂点数VでO(V)、または深さdと平均分岐数bを用いてO(b^d)と記述できます
PV 140
Fav 0
2018.07.22